MuMeta - Mucube and Muoctahedron

30 April, 2023

8-Colouring

17171717

Loop Cycles

\(2\mathord*(t_1-,t_2-)\;\)\(2\mathord*(t_1-,t_4-)\;\)\(2\mathord*(t_2-,t_3-)\;\)\(2\mathord*(t_3-,t_4-)\;\)

Gyre Multipliers

\(-\)

Growth

Single Tile Boundary Vertices

Topology Type

Infinite Genus

Skeleton Type

Primitive Cubic Lattice (pcu)

Files

graphML Download

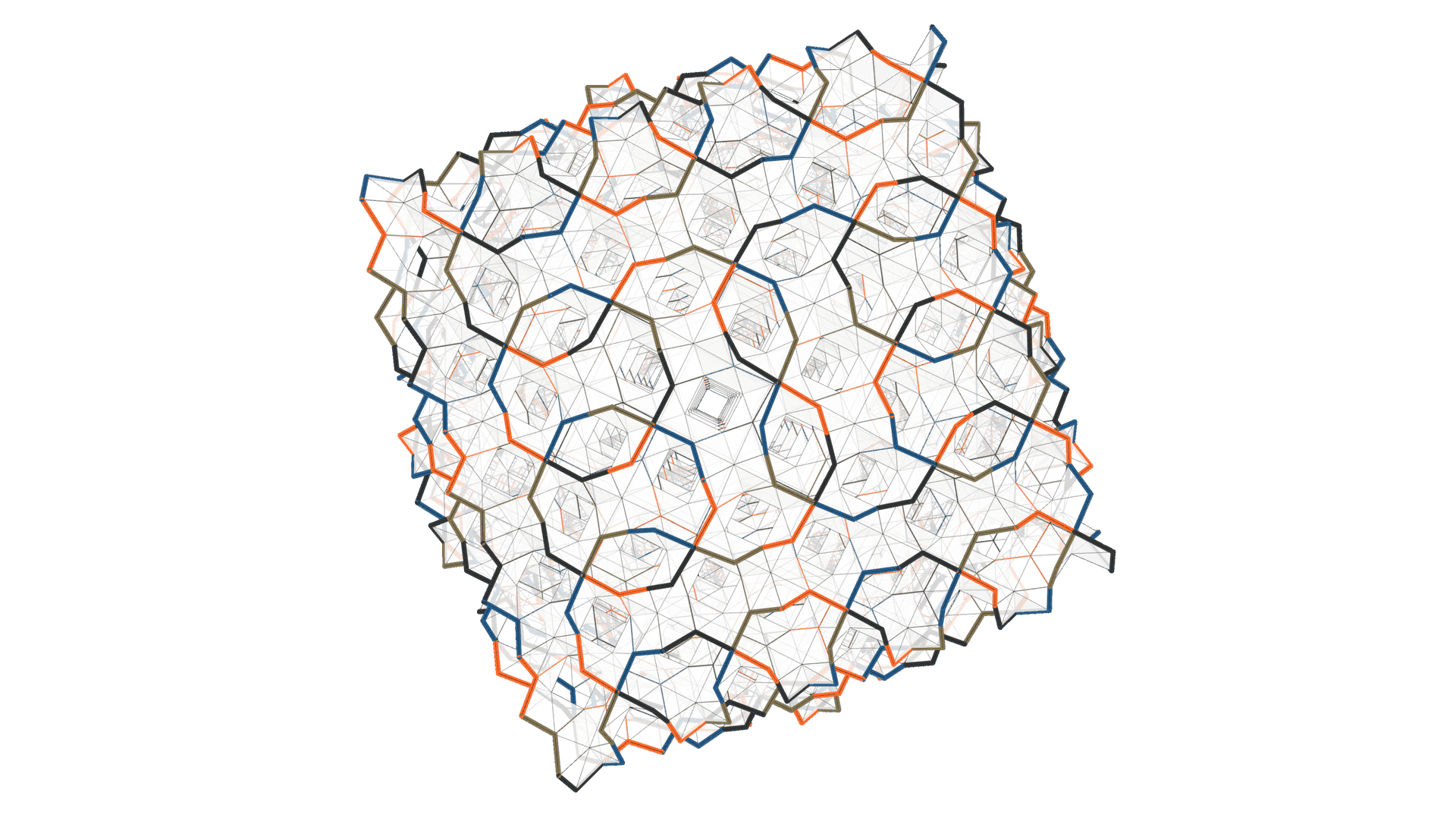
Embedding

Notes

An octagonal structure that can either form the mucube or the muoctahedron based on the tesselation of the tile interior. Read more about this tilegraph here.

Dual Group

\(G_d=\)	\(\left\langle \: S_d \:\middle\|\:R_d\:\right\rangle\)
\(S_d=\)	\({t_1},\:\)\({t_2},\:\)\({t_3},\:\)\({t_4}\)
\(R_d=\)	\({t_1}^{-3},\:\)\({t_2}^{-3},\:\)\({t_3}^{-3},\:\)\({t_4}^{-3},\:\)\({t_1}^{-1}{t_4}^{-1}{t_3}^{-1}{t_2}^{-1},\:\)\(({t_1}^{-1}{t_2}^{-1})^2,\:\)\(({t_1}^{-1}{t_4}^{-1})^2,\:\)\(({t_2}^{-1}{t_3}^{-1})^2,\:\)\(({t_3}^{-1}{t_4}^{-1})^2\)
\(\|G_d\|=\)	\(Infinite\)