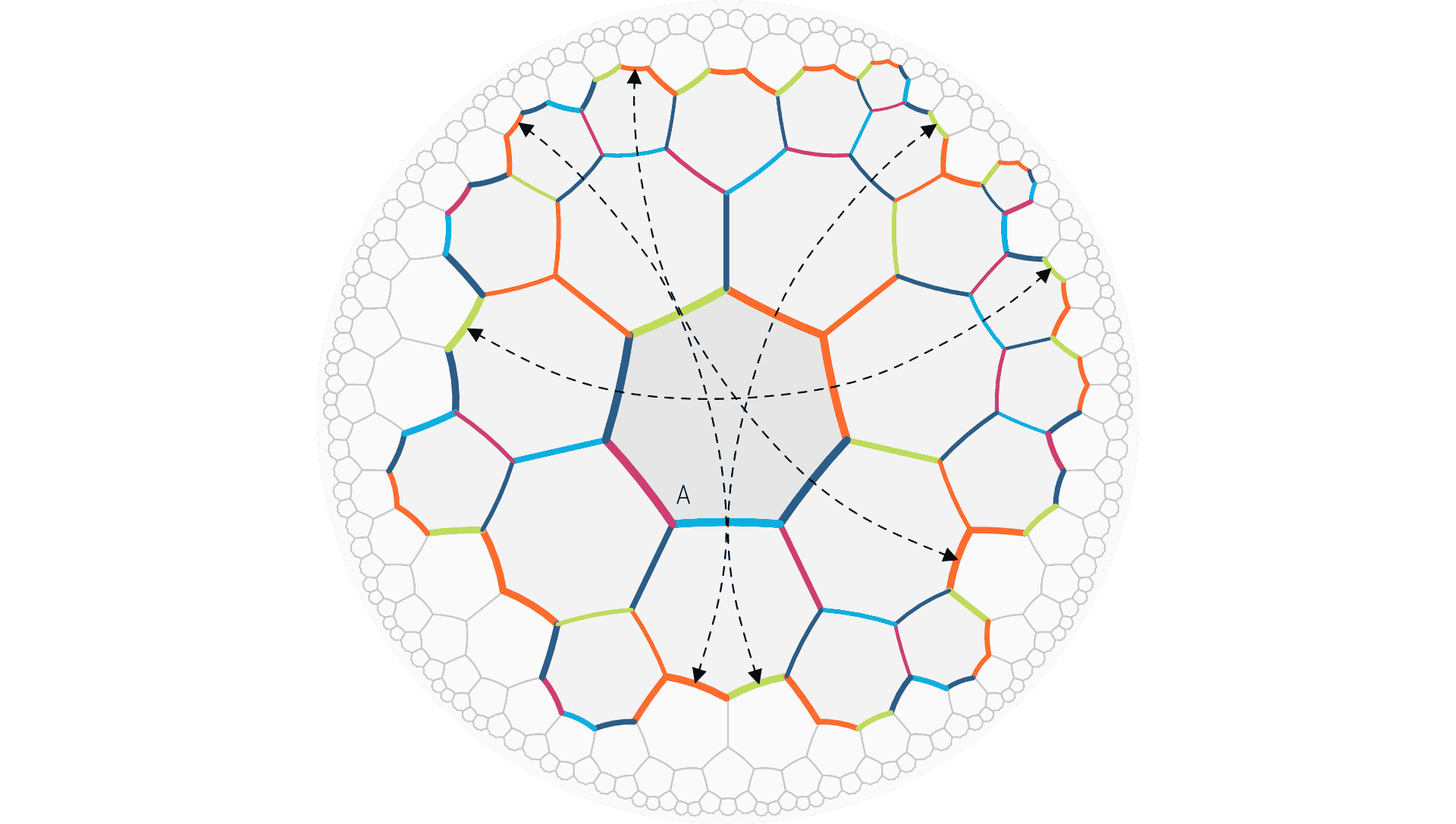
Klein Quartic

A surface tiling well known for its high symmetry. Consisting of 24 heptagonal tiles, it wraps around a tetragonal skeleton and is thus a genus 3 surface. These properties match the Heptagon Tetragonal Wrap I and Heptagon Tetragonal Wrap II. Where it differs is in its single 4-colour loop cycle that manages to twist the tiles into a tilegraph with 168 orientation preserving automorphisms. This matches the upper bound of automorphisms given by the Hurwitz automorphism theorem, for a genus 3 compact Riemann surface.

For more on the Klein Quartic see Wikipedia and John Baez's Page on the subject, which facilitated finding the right loop cycle.