Hendecagonal Triply Periodic I
24 March, 2023
11-Colouring
110031111080401101107
Loop Cycles
Gyre Multipliers
Growth
Single Tile Boundary Vertices
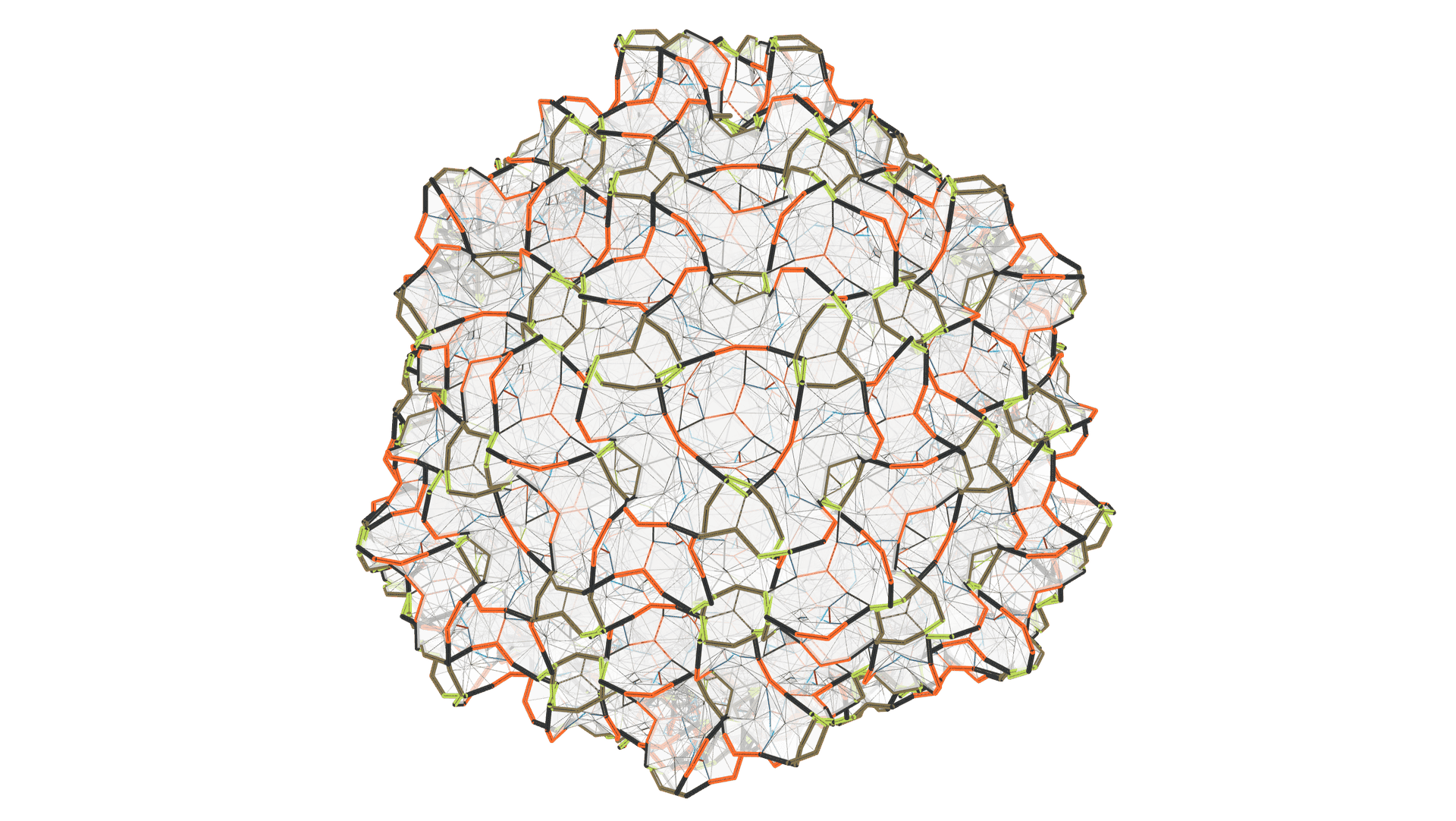
Embedding
Notes
Self-intersecting triply periodic surface tiled by hendecagonal tiles.
Dual Group
24 March, 2023
11-Colouring
110031111080401101107
Loop Cycles
Gyre Multipliers
Growth
Single Tile Boundary Vertices

Embedding
Notes
Self-intersecting triply periodic surface tiled by hendecagonal tiles.
Dual Group