Decagonal Utility Graph Wrap

Decagonal Utility Graph Wrap

03 February, 2023

10-Colouring

1090109050301090705

n-colouring 1090109050301090705

Loop Cycles

\((t_1-,t_5+)\;\)\(2\mathord*(t_2-,t_4-)\;\)\(3\mathord*(t_3)\;\)\(2\mathord*(t_4)\;\)

Gyre Multipliers

\(-\)

Growth

Single Tile Boundary Vertices

Topology Type

Finite Genus

Skeleton Type

Utility Graph

Files

graphML Download

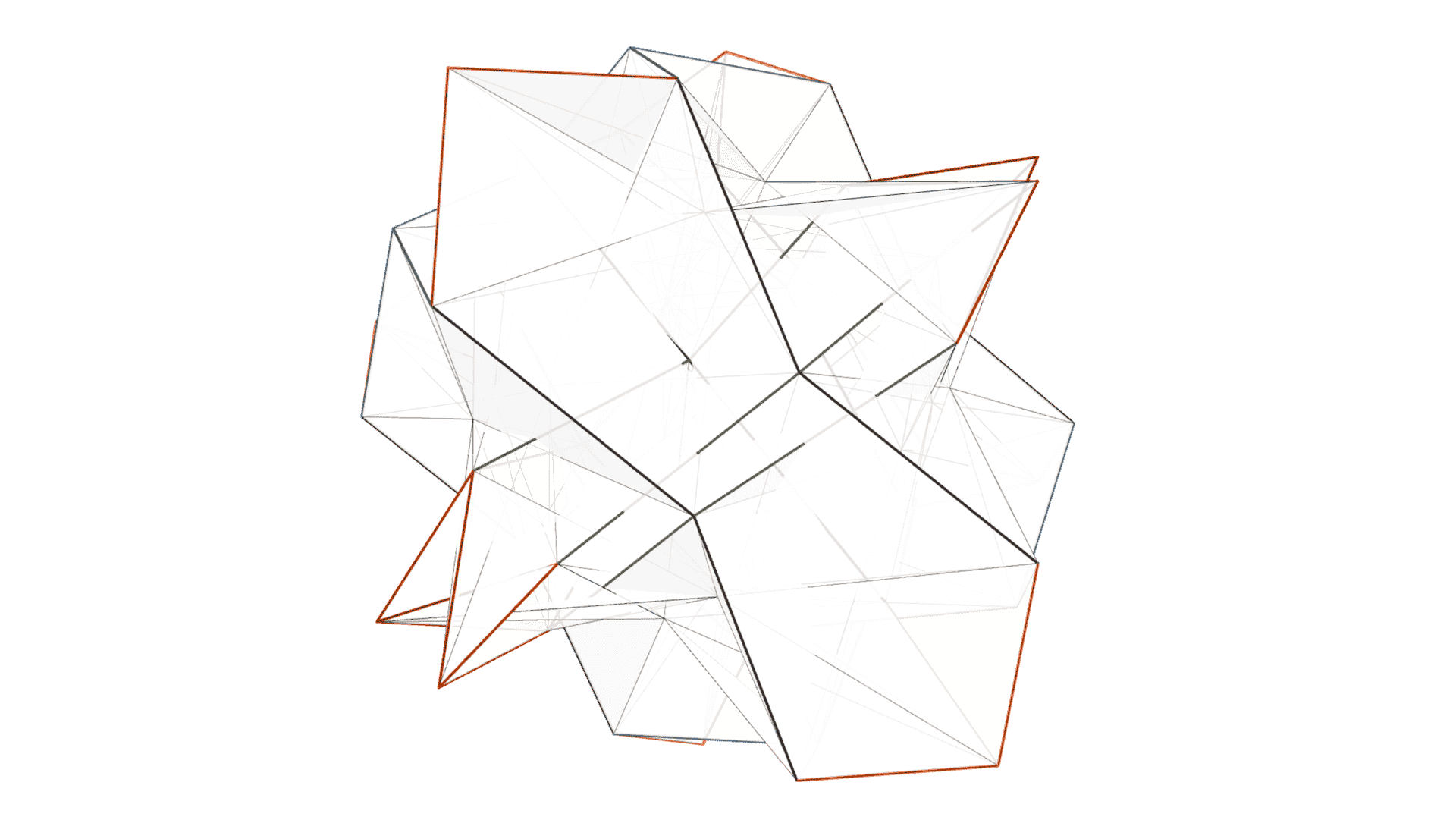
Embedding

Notes

This decagonal tilegraph has a utility graph as its skeleton. The base tile is extremely asymmetric, which makes it quite astonishing that such a tight closed surface can be made out of merely 18 tiles.

Dual Group

\(G_d=\)\(\left\langle \: S_d \:\middle|\:R_d\:\right\rangle\)
\(S_d=\)\({t_1},\:\)\({t_2},\:\)\({t_3},\:\)\({t_4},\:\)\({t_5}\)
\(R_d=\)\({t_1}^3,\:\)\({t_2}^3,\:\)\({t_5}^3,\:\)\({t_1}{t_3}{t_2},\:\)\(({t_4}^{-1}{t_3})^2,\:\)\(({t_4}^{-1}{t_5})^2,\:\)\({t_3}^3,\:\)\({t_4}^2,\:\)\(({t_2}{t_4})^2,\:\)\({t_5}^{-1}{t_1}\)
\(|G_d|=\)\(18\)

Vertex Group

\(G_v=\)\(\left\langle \: S_v \:\middle|\:R_v\:\right\rangle\)
\(S_v=\)\(a,\:\)\(b,\:\)\(c,\:\)\(d,\:\)\(e\)
\(R_v=\)\(a^2,\:\)\(b^2,\:\)\(c^3,\:\)\(d^2,\:\)\(e^2,\:\)\((ad)^2,\:\)\((ae)^2,\:\)\((ba)^4,\:\)\((bd)^3,\:\)\((be)^2,\:\)\((de)^2,\:\)\((bc^{-1})^2,\:\)\((c^{-1}d)^2,\:\)\(acac^{-1},\:\)\(cec^{-1}e,\:\)\(badbab(abd)^2\)
\(|G_v|=\)\(288\)