Bolza Surface

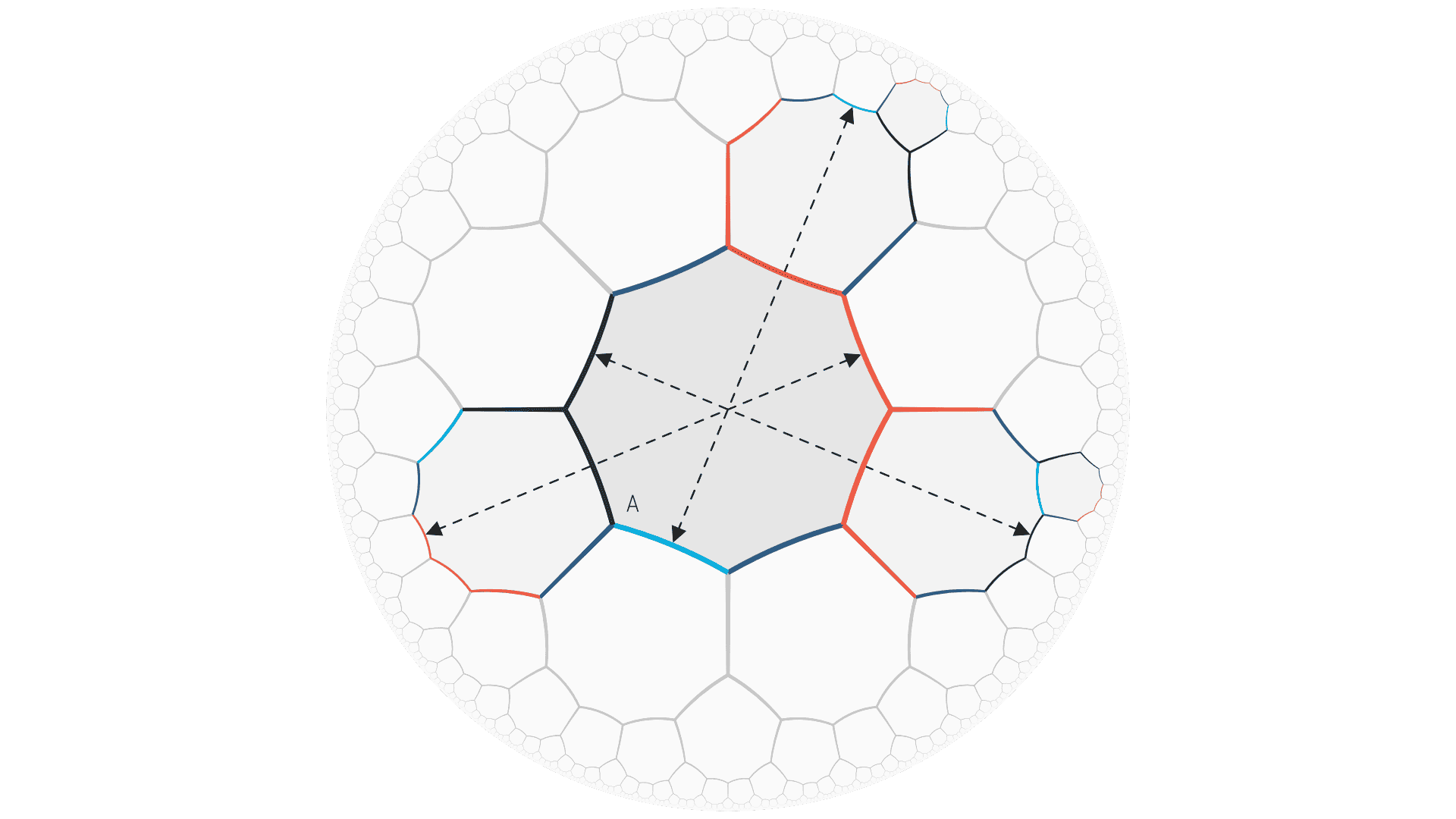
The Bolza surface of genus 2 is highly symmetric, the combination of 6 octagons leads to a tilegraph with 48 automorphisms (if we ignore the colouring and mirror symmetries). It is known to have the most orientation preserving self mappings of a genus 2 surface, although it does not reach the Hurwitz bound $84(genus - 1)$ of maximal possible automorphisms.

Above you will find the unfolded projection of the Bolza surface on the hyperbolic plane with the loop cycles passing through the central tile (A) hinted at by dashed lines. While we only have two loops you will see three crossings. This nicely illustrates how loop cycles going through edges of transpositional colour $(t_1+,t_3-)$ actually result in two crossings of every tile rather than one, due to the defined reversability of loops. Loop cycles must be "walkable" in both directions.

An interesting derivative of the Bolza Surface is obtainable by omitting the loop cycle $(f_1,f_2)$. The result is a tilegraph that can be embedded as a cylindrical regularly punctured surface.

More Information on the Bolza Surface can be found at Wikipedia.