Gyres

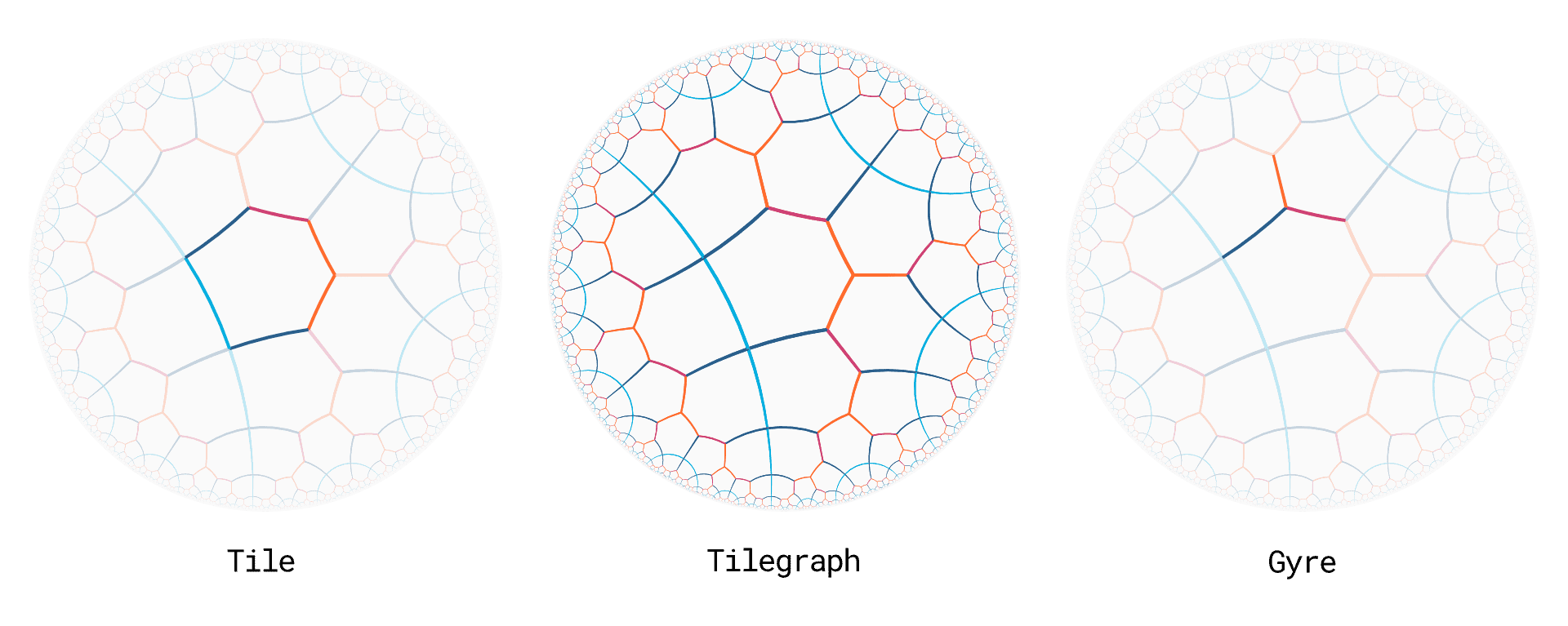
Looking at tilegraphs there are multiple ways one could try to break them down into different components. Two of which you will find illustrated above, Prototiles and Gyres. Both valid in their own right and both mutually informative, with a relationship reminiscent of the two different notations for 2-dimensional combinatorial maps. While we focused on prototiles when describing the glueing and looping rules we will concentrate on gyres in this section and at least initially divert our attention from the colour cycles of single tiles to the colour cycles around single vertices.

We start by more closely examining the somewhat simplified illustration above. In the middle you will find a tiling of the hyperbolic plane by the prototile $t^1t^22f$, the central instance of the tile has been visually isolated to the left. To the right we see what we call a gyre, a set of colored edges that come together at a vertex. In this particular instance the gyre consists of edges coloured KAKI, NAVY and WINE.

Now, as an exercise, try to identify and count the same gyre by walking once around the central tile in the tilegraph. You will see that it occurs three times along with two other gyres along the edge of the tile. A CYAN, NAVY, CYAN, NAVY coloured gyre occurs 2 times and a KAKI, KAKI, KAKI gyre occurs once. By definition the tilegraph consists of instances of the same tile and the glueing rules ensure that these instances are always combined in the same way locally along edges and around vertices, from this we can somewhat loosely deduce that no other gyres will be found in the tilegraph than the ones we have already seen around the central tile. Or more bluntly put, we are able to determine how frequently which gyres will occur in a tilegraph by simply examining its constituting prototile.

For this purpose we have developed the so called gyre graph, but before we dive into its construction, we need to introduce a bit more precision to our illustrations and a few definitions.

Let's zoom in on our gyre example and look at it in detail. Below in the blown up excerpt of our tilegraph, both halves of glued gyre edges are now shown and also the direction of the prototiles' n-colouring. We can thus now define gyres more precisely to be the set of the coloured/directed edges incident to vertices. In our example the gyre consists of 6 edges, 3 incoming and 3 outgoing.

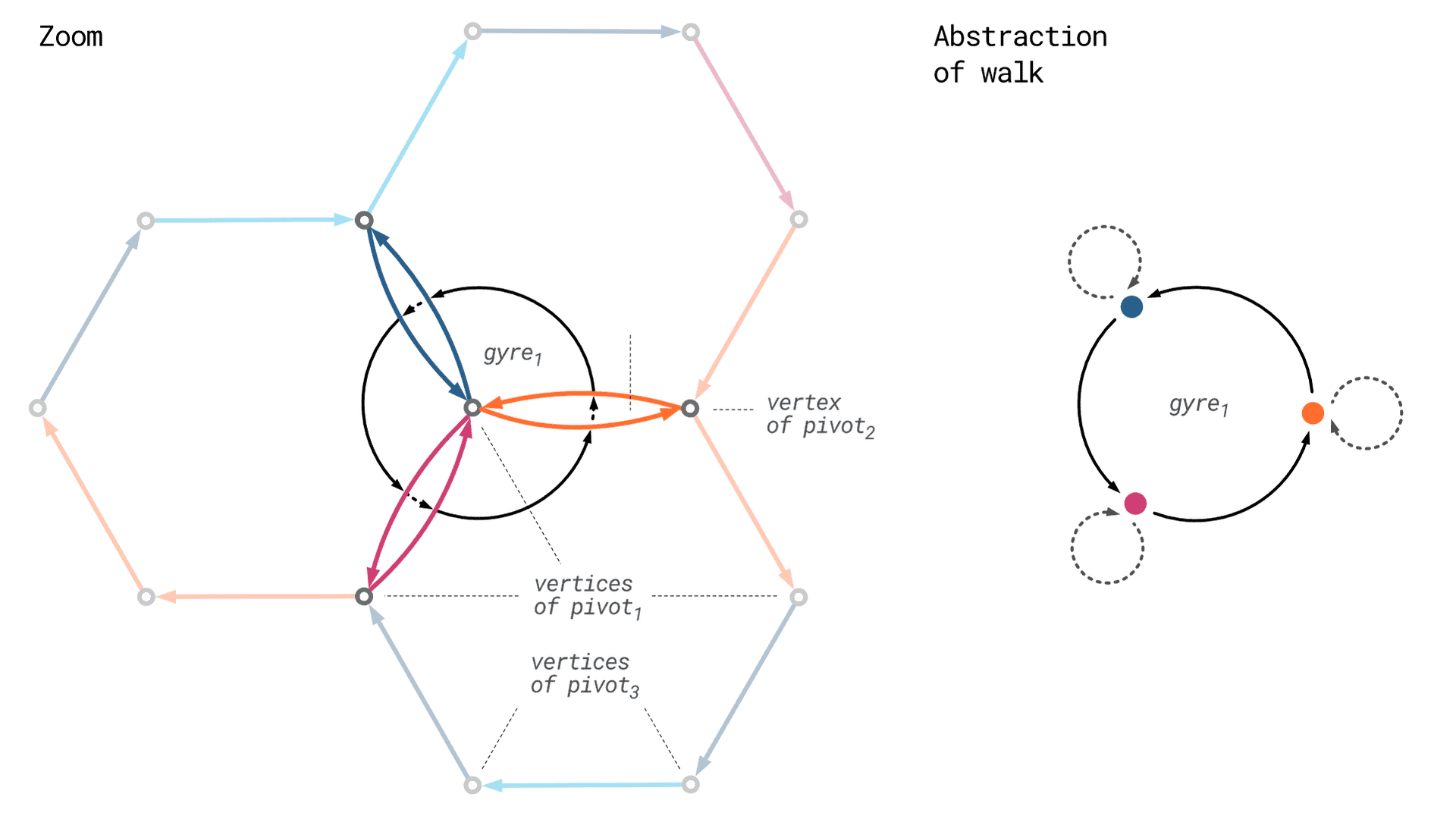
To get a feel for the gyre we can describe it in terms of a circular walk around the vertex we are focusing on. Looking closely, you will notice that each edge crossing of the walk will either take us out of a prototile or onto a prototile. So either we will be walking between two edges of the same tile, that share one vertex, this we will denote as a vertex sharing step, or we will be walking from the edge of one tile to the matching edge of another, which will be denoted as a glueing step. Glueing and sharing steps alternate on our walk. An almost banal observation, but essential none the less. We therefore capture it in the abstraction of our walk to the right by drawing solid arrows for vertex sharing steps and dashed arrows for glueing steps and indicate glued edges by their colour.

Further definitions:

• Pivot - The set of vertices that are at the center of the same gyre, we call the pivot of the gyre.
• Gyre Order - The sequence of edge-colours you encounter on your walk around a pivot, while crossing the tile edges incident to the pivot.
• Monogyre/Polygyre - A monogyre is a gyre consisting of only one transpositional color. A polygyre consists of multiple fixed and/or transpositional colors.
• Gyre Unit The gyre that would be created, if we would loosen the glueing rules a bit and allow consecutive edges of tiles to be glued. Thus the gyre unit will either contain less or the same amount of colours as the regular gyre.
• Gyre Multiplier The gyre multiplier is a natural number that defines how many unit gyres have to be present around its pivot before the zip up rule can be applied. The default gyre multiplier for any gyre is $gm = 1$.
• Gyre Degree The number of prototiles coming together in the vertices belonging to the gyre's pivot or simply the number of outgoing or incoming edges to the central vertex of the gyre.

Based on these definitions, we can make several observations.

• The outcome of the vertex sharing step is uniquely defined by the n-colouring, the outcome of the glueing step is made unique by the glueing rules. Since the steps are uniquely defined, any vertex of a tilegraph can only belong to one pivot or be at the center of one gyre.
• Any fixed colour will always only occur in one gyre.
• Transpositional colours can either occur in one gyre or two.
• The notions of unit gyre and gyre multiplier are particularly interesting for vertices between two consecutive edges of same transpositional color. Unit gyres of any such monogyre would be incident to two tiles only, we can define the number of incident tiles in such vertices to be any number $\mathbb{N} \geq 3$ by means of a gyre multiplier.

With this we are ready to start with the construction of the gyre graph. A gyre graph is a simple instrument that helps expose the combinatorial structure of n-colourings and maps out resulting gyres and pivots.

Since we know that any edge-colour will end up in a gyre and gyres are per definition dependent on the order of the n-colouring, we start our construction of the gyre graph by drawing our n-coloured prototile as an equilateral n-gon, we then proceed to construct the gyres that will occur in any tilegraph grown using our prototile by following the simple steps layed out in the image sequence below.

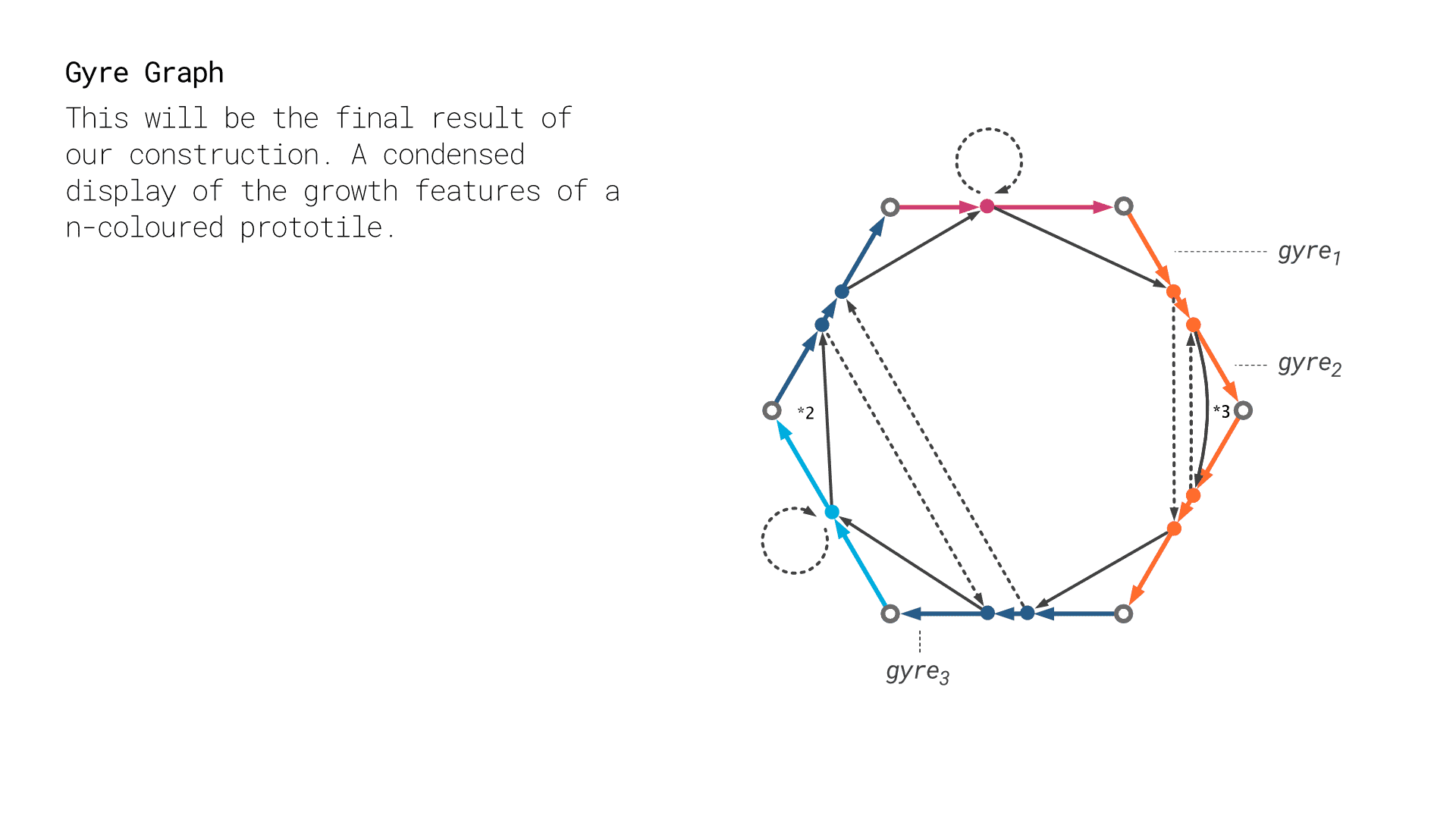
The power of the gyre graph is its ability to visualize the combinatorial structure of n-colourings and resulting tilegraphs in a condensed form. We can easily read the following properties from the gyre graph.

• Gyre Count - The number of different gyres that will occur in a tilegraph can be found by counting the number of closed directed loops of the introduced glueing and sharing edges.
• Vertices of Pivots - The vertices that belong to the pivots at the center of the gyres can be found by simply checking which vertices are "cut off" by the sharing (solid) edges of the gyres.
• Prototile Vertex Incidence - The number of prototiles coming together in a vertex of the prototile can be found by checking which gyre the vertex belongs to and counting the number of sharing (solid) edges of the gyre.
• Gyre Degree - The number of prototiles coming together in a vertex of the pivot of the gyre, can be found by counting the number of sharing (solid) edges of the gyre. Analog to the Prototile Vertex incidence.
• Gyre Proportion - The proportion of the occurence of gyres in a tilegraph can be found by relating the gyre degrees.
• Angle Deficit in Vertices - The angle deficit in a vertex and thus of the overall prototile can simply be found by subtracting the effective angle in a vertex (defined by its gyre degree) $\frac{2\pi}{gyre\;degree}$ from the angle of the equilateral n-gon of the prototile $(n-2)\pi$.

Some of these properties have been captured in the n-colouring tables you can find here.

The gyre graph also amply illustrates the difference between fixed and transpositional colours in the n-colourings. Transpositional colours lead to "shortcuts" accross the prototile and these "shortcuts" are the foundation of the coexistance of multiple gyres in one prototile.

Any n-coloured prototile consisting of only fixed colours will automatically only have one gyre and thus the gyre degree will always be $n$. So fixed coloured prototiles can only create tilegraphs of the kind where the number of edges $n$ of the prototile will be the number of prototiles joined in one vertex. Some examples are the tetrahedron or the square lattice.

As a last bid to further your understanding of gyres, let's have a look at the three different gyres we identified in the gyre graph by showing them in the planar tilegraph tiling the hyperbolic plane. Click through the slides to get isolated representations of the gyre instances in the tilegraph.

You can find more information about gyres by perusing the detailed elaborations in our paper.