Glueing & Looping

Introduction
The intricate structures found in the tilegraph section are generated by applying simple generative rules to a single so called prototile.
Prototiles are abstract polygons with coloured edges. Abstract in this context implies that we do not initially care about the geometry of the prototile, but only about its combinatorial properties. That is, how many edges it has and which colors have been chosen for these edges. Geometry or the embedding of the structure into a 2, 3 or n-dimensional space - using angles and lengths - only comes into the picture after the structures have been created. This has many implications. One being that while many of the models can be built using scissors, tape, paper and tenacity, this is not the case for all models by far. So "Paper is not always your friend", when it comes to exploring tilegraphs. Nevertheless, thinking about the generating process in a haptic way helps develop an intuitive understanding of it. In this basic introduction we will therefore go down that route. If you are interested in a more technical run-down have a look here.
Growing Simple Tilegraphs
Growing your own paper based tilegraph would entail the following steps.
Creating the n-Coloured Prototile
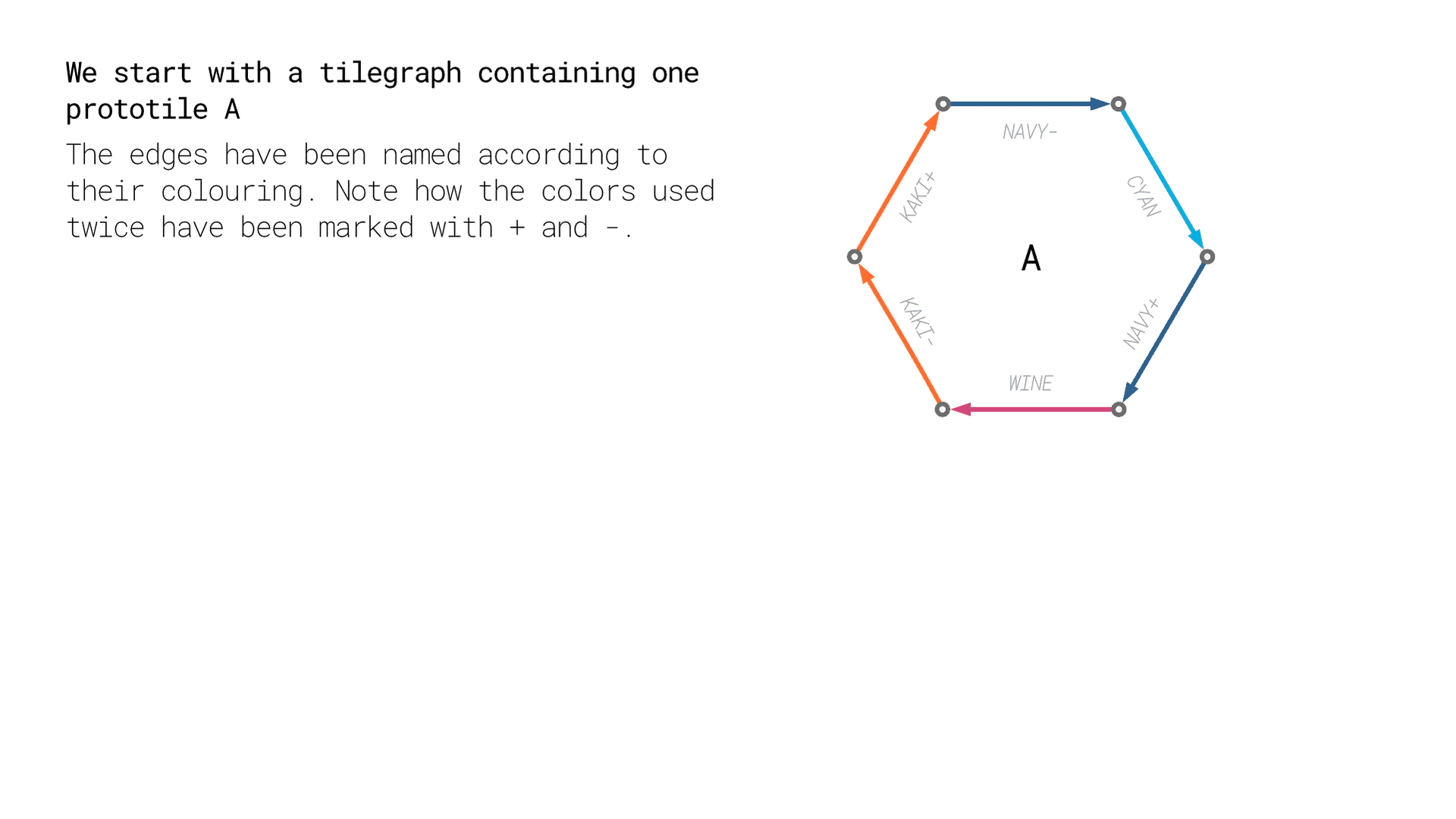
First we create a prototile. Any tiles in the tilegraph we are creating will be a copy of the same prototile.
- Pick a regular polygon as a starting point, for example an equilateral triangle or a pentagon
- Draw a coloured arrow along each edge in such a way that all arrows form a cycle (you are allowed to use every colour only once or twice)
- Mark colours occurring twice with a minus and a plus respectively
The colored polygon is what we will call a prototile, the cycle of colours you have created we refer to as a n-colouring throughout the site and the two types of colours therein we will refer to as:
- Fixed colours - if they occur once
- Transpositional colours - if they occur twice, marked with a $+$ and a $-$ respectively
As you can probably divine from the title of the site, transpositional colours are central to the creation of tilegraphs and make up the core ingredient that allows us to grow the immense diversity of different results seen here.
Below you see three examples of possible prototiles. The leftmost example shows a prototile with three edges all coloured with three fixed colours $f_1,f_2,f_3$. The tile in the middle is coloured with one transpositional colour $t_1$ and one fixed colour $f_1$. To the right you see a 5-sided prototile coloured with two transpositional colours and one fixed colour.
If you are wondering what the cryptic codes in the middle of the prototiles stand for, those are signatures for the n-colourings of the prototiles. A universal naming system was developed for the n-colourings so that any possible n-colouring can be uniquely identified, whether it colors prototiles of 3,4,5 or a 100 edges. Go to n-colourings to browse through the coloured prototiles of up to 10 edges. In all our diagrams we always use the same colors in the same places. A color code reference can be found here.
Combining Tiles
Now that we have a prototile and hopefully several copies of it, we need to know how they can be combined. We differentiate between two different sets of rules that govern how tiles are allowed to be connected.
- Glueing rules - that will tell you how you are allowed to add a tile to a tilegraph
- Looping rule - that will tell you when to connect the tilegraph to itself
The Glueing Rules
How do tiles go together? It is quite simple.
- Glue - You are allowed to glue together edges of the same colour, with the slight restriction for transpositional colors that only $+$ goes with $-$. No $-$ with $-$ and no $+$ with $+$. Think of transpositional colors as being magnetic: like poles repel each other, opposite poles attract.
In the same spirit make sure you align the connected edges in such a way that the arrows you drew point in opposite directions. This ensures that the tiles are always oriented with the same side up and down.
- Zip-up - Once you have connected a new tile to a tilegraph via a matching colour you need to follow through and zip-up any further matching edges. Imagine a two way zipper starting at the freshly glued edge that zips up any consecutive matching edges. Consecutively zipping up multiple edges of the same two tiles is not allowed though.
You will see, the glueing operation comes quite naturally when you have the tiles in front of you, so let us have a look at an example. Click through the slides below to see how three hexagons of type $t^1t^22f$.
As you can see in the example the vertex at the center of the final tilegraph evidently has 3 neighbouring tiles (A, B and C). This will not be true for all vertices. Take for example the vertex shared by the CYAN edge of B and C. It is obvious that you will need to add more than one further tile around that vertex to uphold the rules, since the prototile does not have two consecutive CYAN edges. To learn more about how we can predict how many faces come together in one vertex throughout a tilegraph, have an in depth look at the concept of gyres here.
Admittedly, the prototile of the hexagon example above will give you some headaches when trying to build paper models based on it that contain more than 3 tiles. If you are looking for some simple examples. Have a look at the cube, the tetrahedron or the rhombic dodecahedron for tilegraphs that close up. For a "wavy" tilegraph you can continue to build to infinity try your luck with flat jaws.
What all these tilegraphs have in common is that they do not contain any loops. By adding tile after tile to them, they will either end up as a closed sphere-like surface where no further tiles can be added or as an endless warbled plane with a bigger and bigger boundary to glue further tiles to.
In order to get loops in our tilegraphs, we at some point need to glue the tilegraph to itself.
The Looping Rule
More or less any tilegraph can be looped by glueing it to itself, as long as the glueing obeys the glueing rules already discussed. Choose any two matching edges of a tilegraph, glue them together and you will end up with one or more loops. While the choice of matching edge pairs could of course happen randomly, we are interested in building replicable tilegraphs.
In the way the n-colouring defines how prototiles can be joined, we want to be able to specify how loops will be created when a specific tilegraph is being built. The way we do this is very similar to how we define the n-colouring of a prototile. We specify sequences of edge colours which would have to be crossed, when walking in a loop on the tilegraph. Such edge sequences we call loop cycles. By convention we always note the edge colour where we exit a tile in the loop cycle. The loop is undirected meaning we should be able to walk it forwards or backwards and end up in the same place and it does not matter with which colour we start in the cycle, we still should end up in the same place.
The looping rule now says that, whenever a tile is added to a tilegraph we need to glue the tilegraph to itself, if this would create one of the defined looping cycles.
Let's go through an example. We define a loop cycle $(f_2,f_3,f_2,f_3,f_2,f_3)$ for our tilegraph. When adding a new tile to the tilegraph we will first glue the edges using the glue and zip-up operations.
Now move your finger - starting from the freshly added tile - from coloured edge to colour edge, going forward in the loop cycle until you end up at an unglued edge. Make a note how far you got. Now do the same thing moving backwards in the loop cycle, again starting from the freshly added tile. If the colours you crossed with your finger can be combined to create the loop cycle sequence, glue the two tiles at the end of your finger walks together at the matching colour and perform the zip-up, if possible. Remember the freshly added tile can be at any place in the loop cycle, so you might have to repeat the finger exercise starting at different places in the cycle.
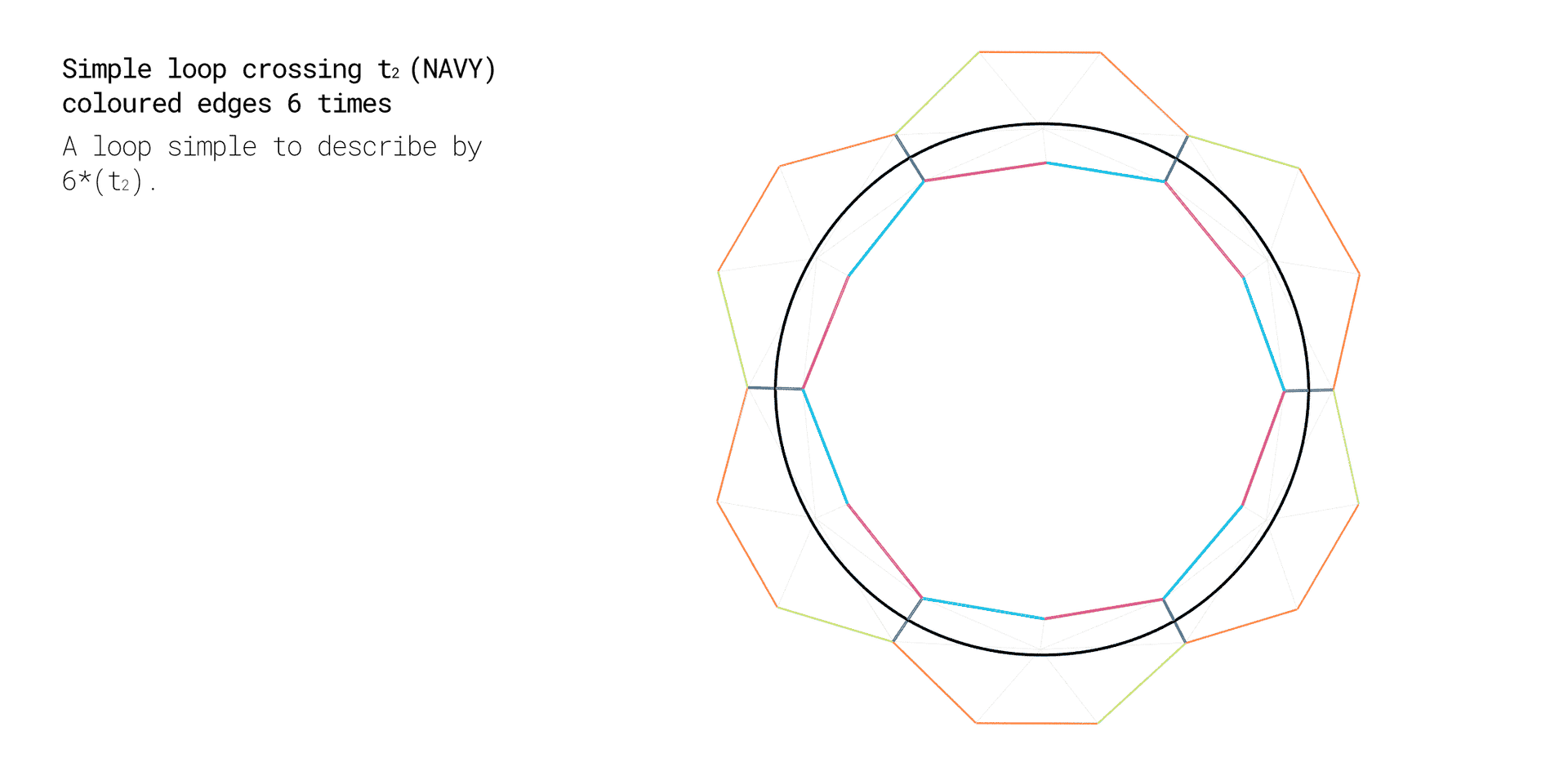
Below you see an illustration of the effect of first one, then two loop cycles for a tilegraph of heptagonal prototiles.
Putting it all together
With n-coloured prototiles and looping cycles, we have the basics together to grow tilegraphs, so let us have a look at a more complex example.
We choose the n-colouring $t^1,t^2,f$ for our pentagonal prototile and two loop cycles: $4*(t_2)$, $2*(t_1+,t_1+,f)$ and decide to grow our tilegraph starting with one tile and continuously adding further tiles along the open boundary of the tilegraph.
To see what happens click through the slides below which show two different representations of the same tilegraph. To the left the tilegraph was embedded into 3 dimensions, to the right it was projected into the hyperbolic plane. Whenever loop cycles come into play, relevant tiles will be marked. Towards the end a couple of steps were skipped to give you an impression of the tilegraph after the addition of 68, 171, 359 and 631 tiles.

This was a rough introduction into the basics of creating what we call transpositional topologies. Quite some details have been left out, but by following the explanations above, you should already be able to understand how the structures come about. If you are interested in diving deeper, please have a look at our more detailed paper.