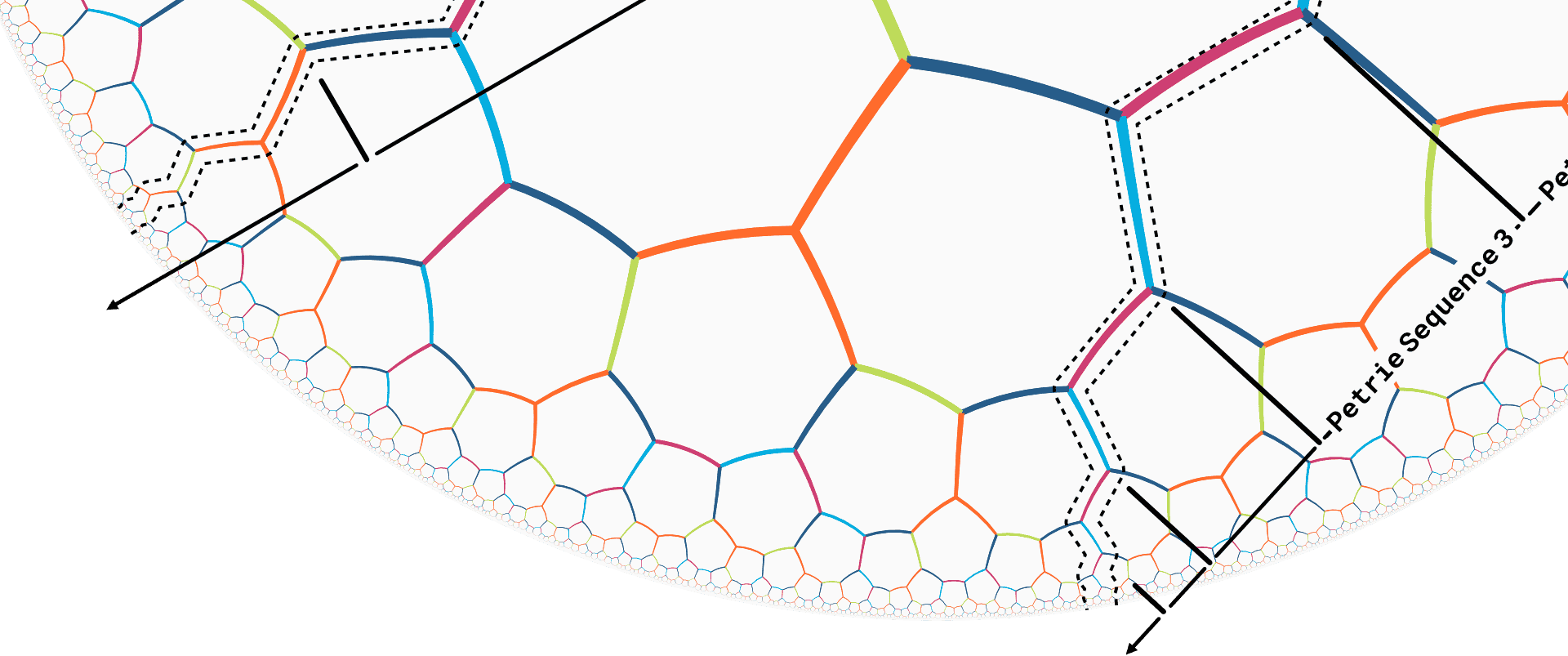
Petrie Paths Along Tilegraph Edges

In Regular and Quasi-Regular Polytopes Coxeter writes the following about Petrie polygons: "It may alternatively be defined as a skew polygon such that every two consecutive sides, but no three, belong to a face of the regular polyhedron.".

In Regular Skew Polyhedra In Three and Four Dimensions also by Coxeter, the concept is described from a different perspective as a circular walk on the edges of a polyhedron where a Flaneur alternatingly takes right and left turns at each vertex.

The "left" and "right" movement of the latter description automatically presupposes that any tilegraph, we might want to examine, would be embedded in a certain way with quite strict local restrictions. If we for example were to randomly draw the nodes of a tilegraph in a plane, every new random drawing would potentially yield other left/right paths along the graph. Thus focusing on the first mentioned definition of Petrie polygons with its emphasis on faces/tiles seems the most obvious choice in the combinatorial context of transpositional topologies. Nevertheless, we will see that the idea of moving along a path by alternating the direction taken at its forks equally has its benefits.

Let's begin by looking at the first two edges of a Petrie polygon in a tilegraph and say they will run in the direction of the n-colouring cycle of a tile $A$. After two steps around $A$ we are not allowed to take a third, so we will need to switch to tile $B$ with whom tile $A$ shares the edge of step 2.

In tilegraphs, tiles which share an edge have by definition been glued together with their edge cycles pointing in opposite directions. Thus to continue and not directly return to the starting vertex of the previous edge, we will now need to move one step against the direction of the n-colouring cycle of tile $B$ to complete the two steps around it and switch to tile $C$. On the edges of tile $C$, we again find ourselves walking along the direction of the n-colouring. In this way, we end up with a succession of steps along and against the direction of the involved tiles' n-colouring cycles or in other words with a sequence of colors which defines the Petrie path. One could say that "left"/"right" movement has actually been replaced by a corresponding back and forth movement along the n-colouring cycle of a tilegraph.

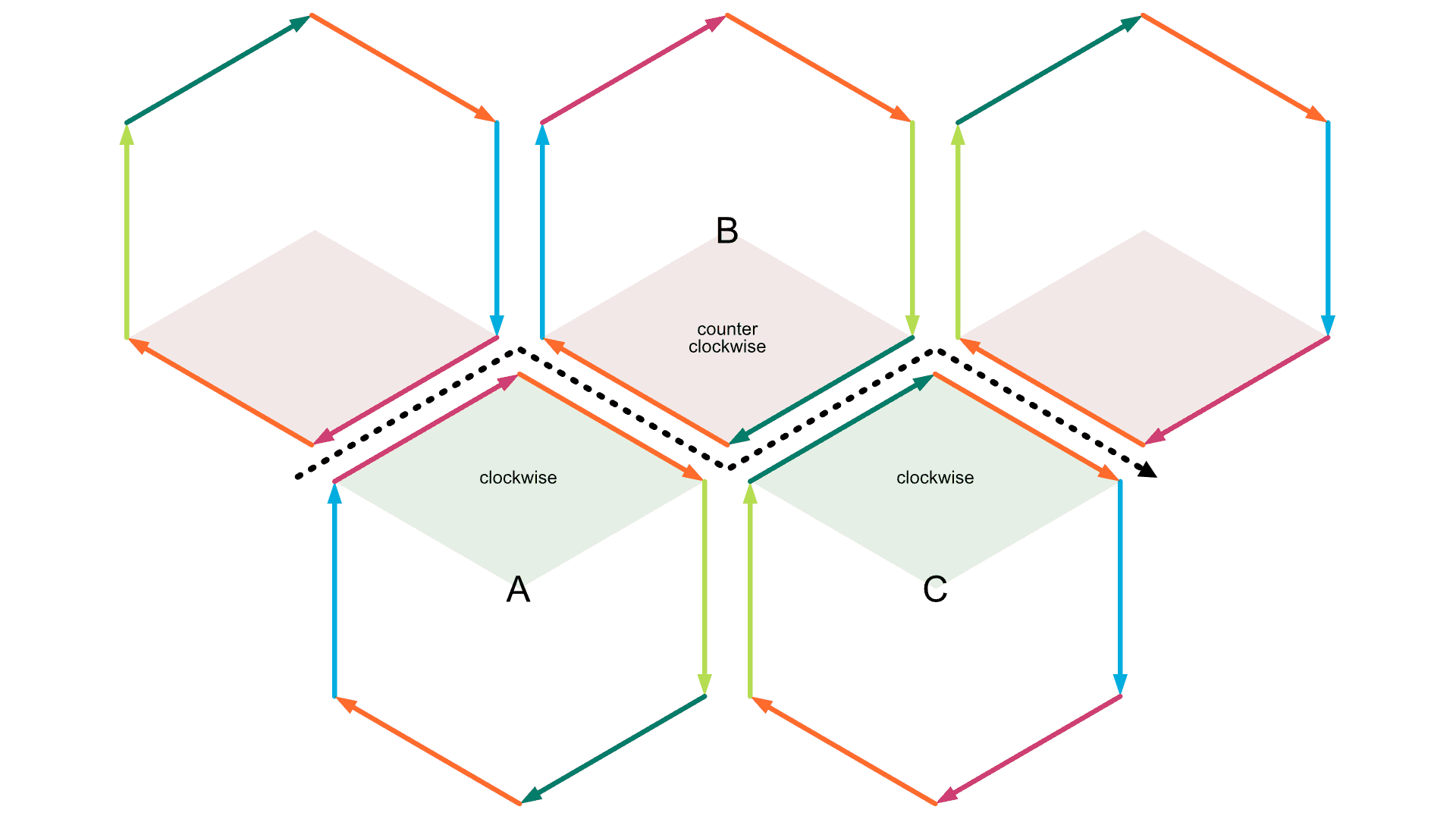
The following observations can be made about the Petrie path color sequence.

Uniqueness Any Petrie path color sequence and thus any Petrie path in tilegraphs is uniquely determined. Based on the previous two colors in the sequence there is only one valid choice for a following color.

Cycle of Cycles Because of uniqueness and because there is a limited set of colors, any sequence will at some point start to repeat. We will refer to the repeating subset of colors as the Petrie Cycle Sequence and to the full Petrie path as the Petrie cycle repetition.

Tile Determination Due to the assertions above Petrie Cycle Sequences are uniquely determined by the coloring of the chosen basetile n-colouring.

Fixed Color Local Mirroring In a Petrie Cycle Sequence the color preceding and following a fixed color will always be the same, while this is not the case for transpositional colors, since a transpositional tile switch takes the Petrie Cycle Sequence to another position in the tile n-colouring cycle.

Sequence Length is Always Even Petrie Cycle Sequences will always have an even number of elements. Since by definition any two consecutive colors in the sequence always differ. This can also be seen as a correlate to the definition that you always need to switch between the two directions left and right.

Multiple Sequences & Sequence Lengths A n-colouring can give rise to one or several Petrie Cycle Sequences. Two consecutive fixed edges will for example always form a sequence containing those two colors and thus for any n-colouring with $n>2$ and more than two fixed colors, there will be more than one sequence. A n-colouring can give rise to one or several Petrie Cycle Sequence lengths. Only if the basetile contains transpositional colors the Petrie Cycle Sequences can have lenghts $>2$.

Infinite Sequences In non-looped infinite tilegraphs all sequences will be infinitely repeated.

Finite Sequences In looped infinite tilegraphs, sequences can be infinitely or finitely repeated. In the case they are finitely repeated the length of the path will be multiples of the number of colors in the repeated sequence. Finite tilegraphs will always have finitely repeated sequences.

Duality The Petrie Cycle Sequences of a tilegraph correspond to the colored Poincaré duals Petrie Cycle Sequences.

Armed with the observations above, we now have a potent tool at hand, that allows us to predict the possible lengths of Petrie Sequences in a looped tilegraph based solely on the choice of a n-colouring.

As an example, lets say we look for n-colouring candidates that would allow us to form a certain regular orientable map.

Regular orientable maps can be classified using an extended Schläfli notation ${p,q}_r$ where $p$ is the number of sides of a face, $q$ the number of faces at any vertex and $r$ the number of edges in the Petrie polygon. From this notation it implicitly follows that "regularity" in the orientable maps only comes with petrie polygons of equal length given by one index $r$.

It has to be remarked though that not every orientable map that can be described by the Schläfli notation above is necessarily regular, further conditions like for example flag transitivity have to be met. For more on the subject see Marston Conder and P. Dobcsányi, Determination of All Regular Maps of Small Genus. Also it is important to state that several different graphs can exist with the same Schläfli notation.

Nevertheless, in the framework of transpositional tilings, in order to create a potential candidate for a regular orientable map defined by ${p,q}_r$ using glueing and looping, we will need to pick a tile where its uniquely defined Petrie Cycle Sequences $s_1,s_2,...,s_n$ must fulfill the requirement of $LCM(s_1,s_2,...,s_n,r)=r$. Furthermore, at first glance the tile will also need to have $p$ sides and all gyres would have to be of order $q$. The two parameters $p$ and $q$ are freely interchangeable though, as can be seen by pondering what such a switch actually means: A change of perspective from the graph of the orientable map to its dual, which leaves the lengths of the petrie polygons in place, since any edge of a petrie polygon of our original map will be crossed by an edge of the petrie polygon of its dual. See also our reference to duality above.

Let's get more specific. Marston Conder has a list of regular orientable maps of genus 2 to 101 and we pick the regular map indexed with R3.1 of Type ${3,7}_8$ which has 336 Automorphisms including reflexions. It corresponds to the well known and thoroughly studied Klein Quartic.

Since ${3,7}$ tiles do not occur naturally amongst 3-colourings, we look towards ${7,3}$ and the 7-colourings for alternatives and end up with only two possible candidates:

$t^1t^33f$ and its mirror $t^1ft^32f$, which both have 7 edges, gyres of length 3 and Petrie Cycle Sequence lenghts of 8, 4 and 2, which obviously fullfill the requirement $LCM(8,4,2,r)=r$ for $r=8$.

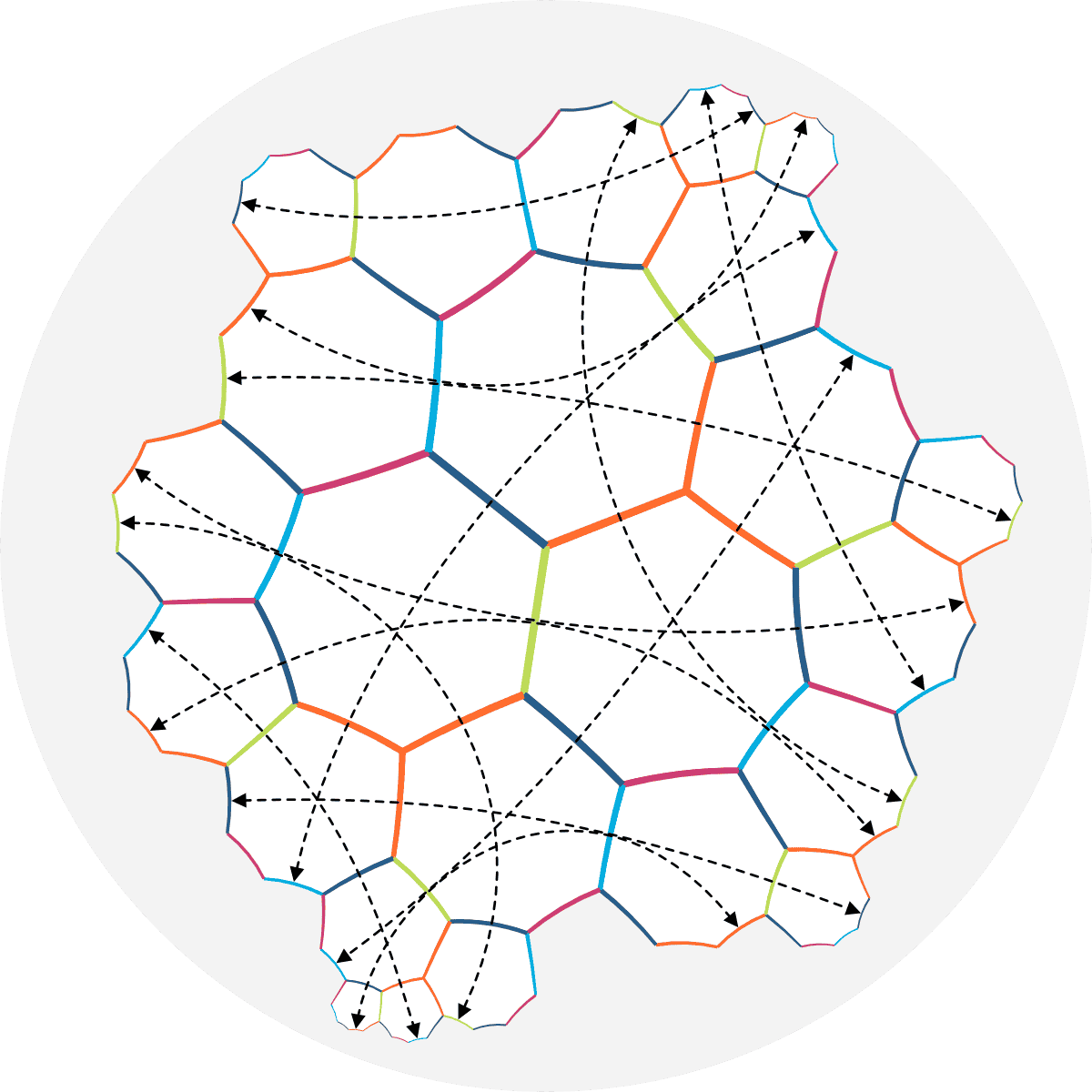
Since the two 7-colourings are mirrors of each other, it does not matter, which one we pick and we go for $t^1t^33f$. To get an idea of the different Petrie Cycle Sequences it is always helpful to have a look at a rendering of the basic looping rule free tilegraph embedded in the hyperbolic plane. The different Petrie Cycle Sequences have been marked in the illustration below. As a fun exercise, try different "left/right" walks starting at any node to validate the claim, that no other than the marked Petrie color sequences can be found.

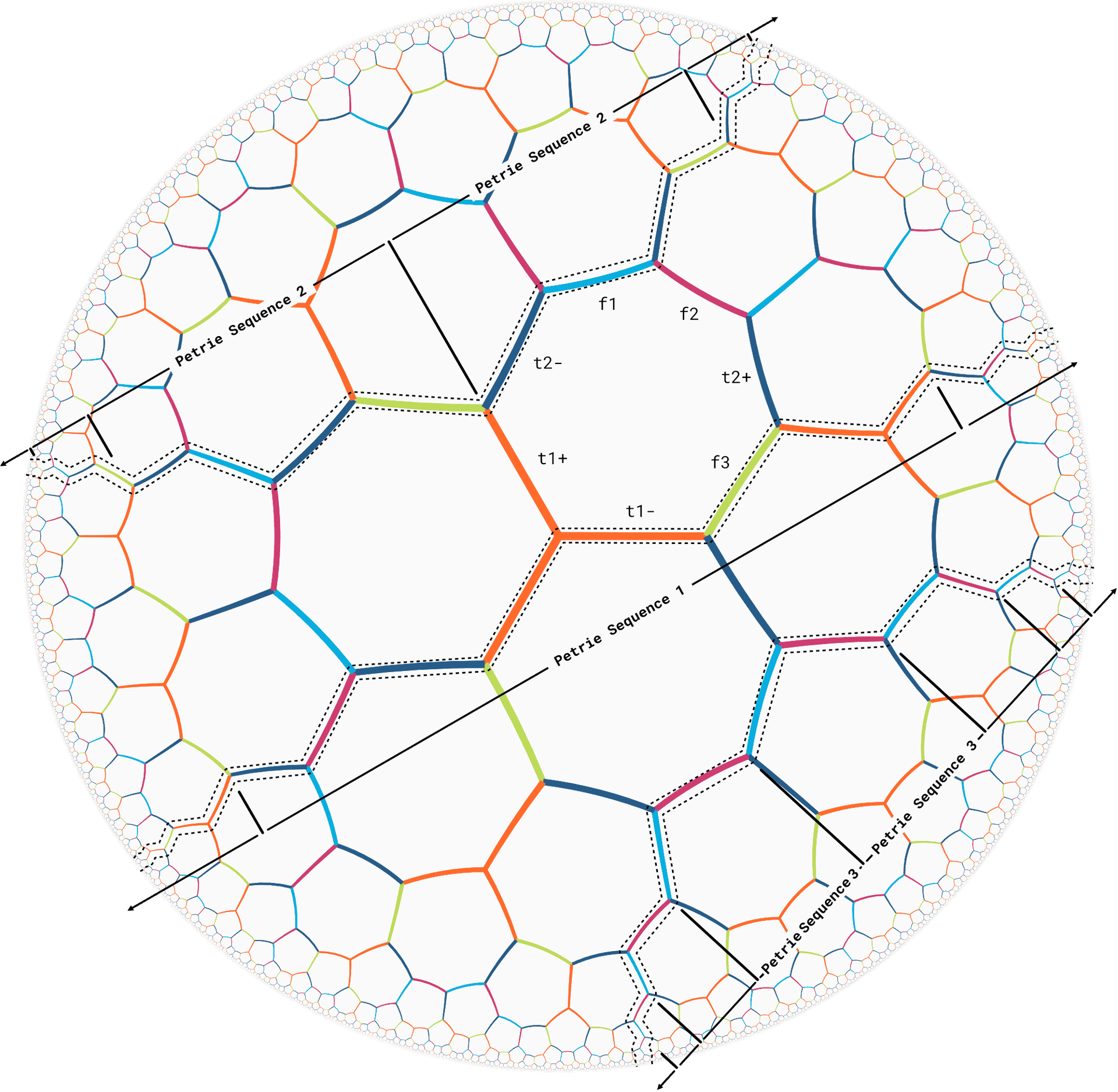
We can easily list the different petrie cycle sequences:

• Petrie Cycle Sequence 1 is $t_2+,f_2,t_2-,t_1+,t_1-,f3,t_1+,t_1-$
• Petrie Cycle Sequence 2 is $t_2+,f_1,t_2-,f_3$
• Petrie Cycle Sequence 3 is $f_1,f_2$

Now we need to look for loops, that form Petrie Cycle Sequences into petrie polygons (loops in their own right) of 8 edges rather than such of length 16, 24 etc.

How to choose such loops is still a matter of ongoing research.

What can be said already though: It is not sufficient to just use the petrie sequences as a looping rule, when growing the tilegraph. As a matter of fact, it appears as if simply tracing the color sequence of the petrie path is an anti-pattern, that almost always leads to degenerate tilegraphs.

This is astonishing, when we recall that the Petrie color sequences of the dual are an exact match of and add the fact that the colored dual of the tilegraph is actually a cayley graph.

Rather than following the color sequences created by the edges, of which the Petrie Sequences are one example, it seems that cross tile sequences are more suitable as a basis for looping rules. In our particular example, after some fiddling, we choose the edge colors before and after the 2 consecutive colours of the longest Petrie Cycle Sequence and see where it takes us. See illustration below.

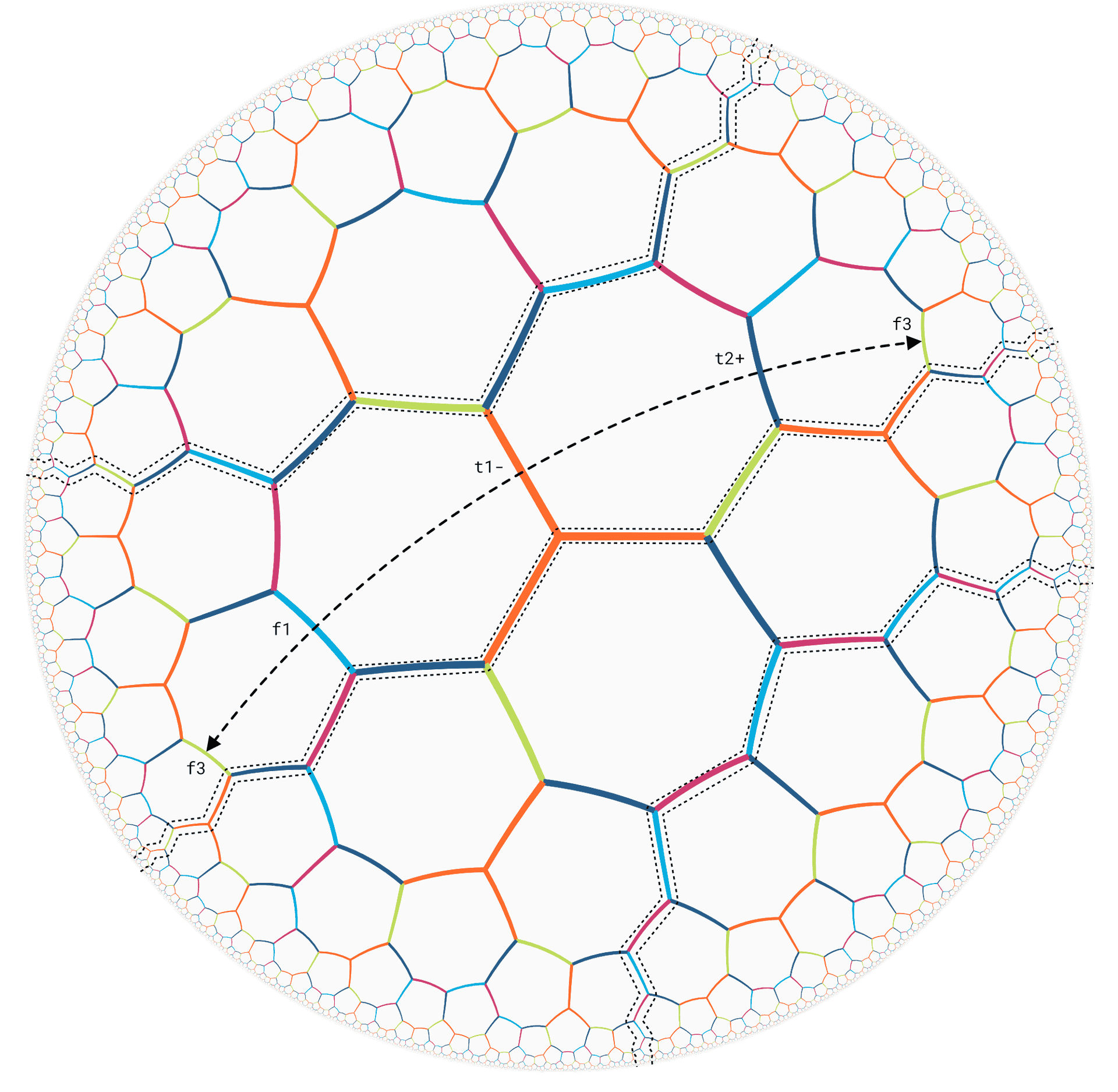
The above gives us a looping rule of colors ${f_3,f_2,t_1-,t_2+}$ that will definitely result in looping our Petrie Cycle Sequence 1 once. The effect on the sequences 2 and 3 is less apparent, but growing the tilegraph with only this simple looping rule, we find that it actually suffices and neatly creates a Klein Quartic Tiling. How can that be?

First have a look at the tiling unfolded in the hyperbolic plane with our looping rule indicated by arrows in such a way that all tiles are least part of one loop cycle. Can you find missing loops? Unfortunately, if you were to try and fold this the good old paper and scissors way, by glueing heptagons together and making the arrowheads meet, this is near impossible in the real world since the resulting surface will be notoriously twisted.

Now what happened to the Petrie Cycle Sequences 1 and 2? Wouldn't we need to define a looping rule for them as well to bound them to 2 respectively 4 repetitions?

Luckily for us our initial rule already takes care of that. Here is how.

In the illustration below we have selectively drawn 4 loops. The edges $A1$, $A2$, $A3$ and $A4$ correspond to the edges $A1'$, $A2'$, $A3'$ and $A4'$. The loops and the drawing of the flattened tiling have been chosen in such a way, that the boundary of the flattened tiling contains the petrie cycle sequences 2 and 3.

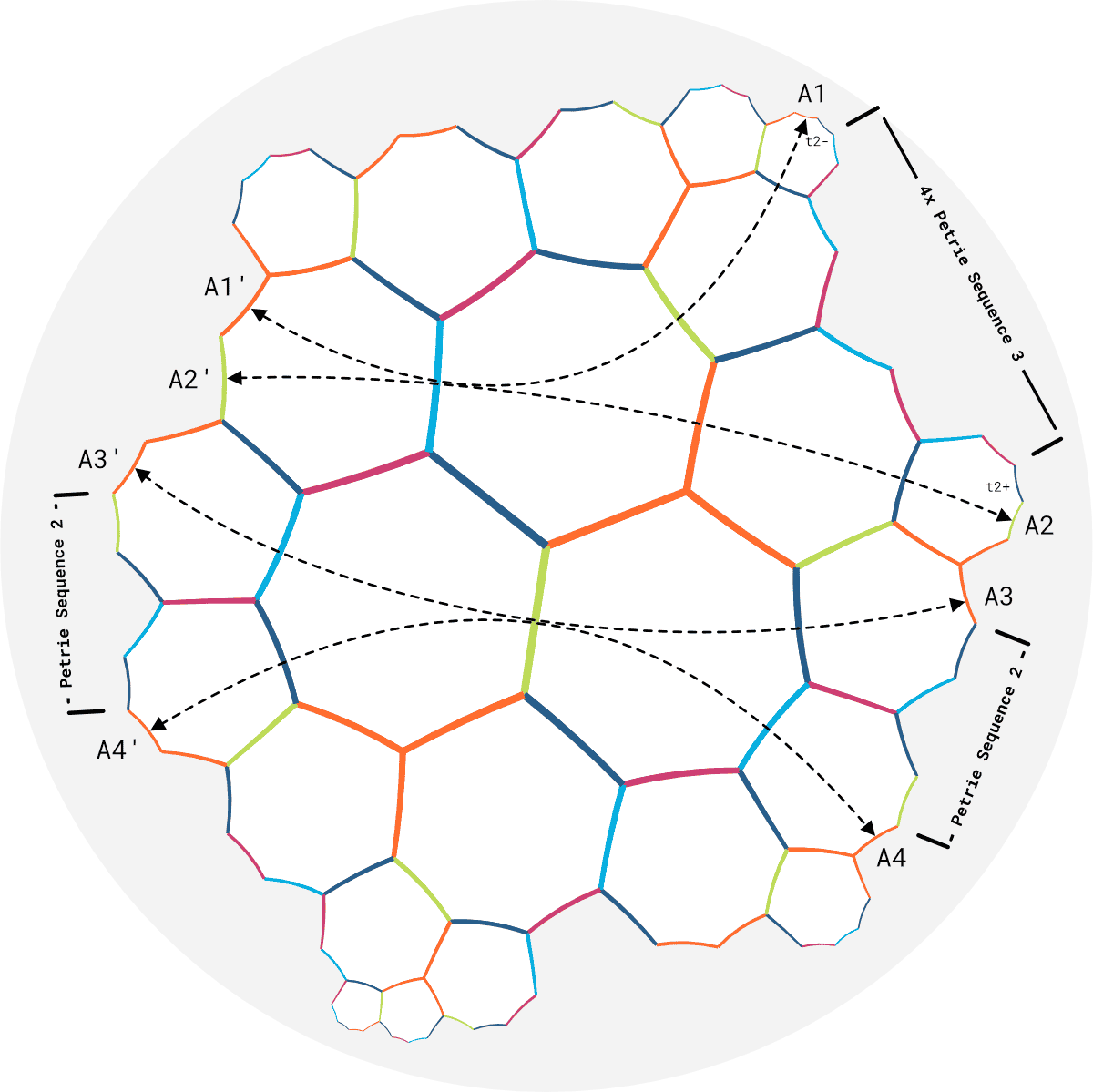
Focusing on petrie cycle sequence 3 we now imagine what happens when we glue edge $A1$ to $A1'$ and $A2$ to $A2'$. The incident edges $A1'$ and $A2'$ will be become incident with the $t_2$ colored edge next to $A1$ and $A2$ to form a full gyre after the glueing. What is left is an opening consisting of 4x "petrie sequence 3"-colored edges and get a total length of 8. Similarly, if we glue edge $A3$ to $A3'$ and $A4$ to $A4'$, we find that the edge color sequence along the boundary between $A3$ and $A4$ is exactly the same as the sequence between $A3'$ and $A4'$ and corresponds to petrie cycle sequence 2. We thus end up with an opening of 2x "petrie sequence 2"-colored edges also of length 8.

With that, we are at the end of the Klein Quartic example. As mentioned, much is still to be explored. Especially, regarding how to pick looping cycle rules. Hopefully more on that soon.

If you want to learn more about the Klein Quartic have a look at Greg Egan's writeup here.

Another interesting and publicly available paper by Coxeter, with a slightly more geometric take can be downloaded here.

I would like to thank Chaim Goodmann-Strauss for pointing out the usefulness of Petrie polygons as a tool for classifying tilegraphs and relating them to other classification schemes of topological structures. His suggestion to look into "Twisted Honeycombs" as described by Coxeter led to the research above and consequentially to some at least to me rather surprising findings.