MuMeta - from Mucube to Muoctahedron and Back

The mutetrahedron - linking six hexagons around each vertex, the mucube - arranging six squares around vertices, the muoctahedron - combining four hexagons around each vertex. All are classic examples of infinite polytopes.

Because of their regularity and due to the extensive coverage their geometrical and combinatorial properties have enjoyed since their discovery (see "Regular Skew Polyhedra in Three and Four Dimension, and their Topological Analogues", Coxeter1938), they are obvious choices when looking for examples of apeirohedra to describe using the combinatorial methods illustrated here.

Finding solutions for the mutetrahedron (tile $6f$ and looping cycles $(f_1,f_3,f_5)$ and $(f_2,f_4,f_6)$) and for the muoctahedron proved to be quite an easy endeavour (tile $t^2ft^2f$ and looping cycles $4*(t_1)$,$4*(t_2)$, $2*(f_1,t_2+)$ and $2*(f_2,t_1+)$).

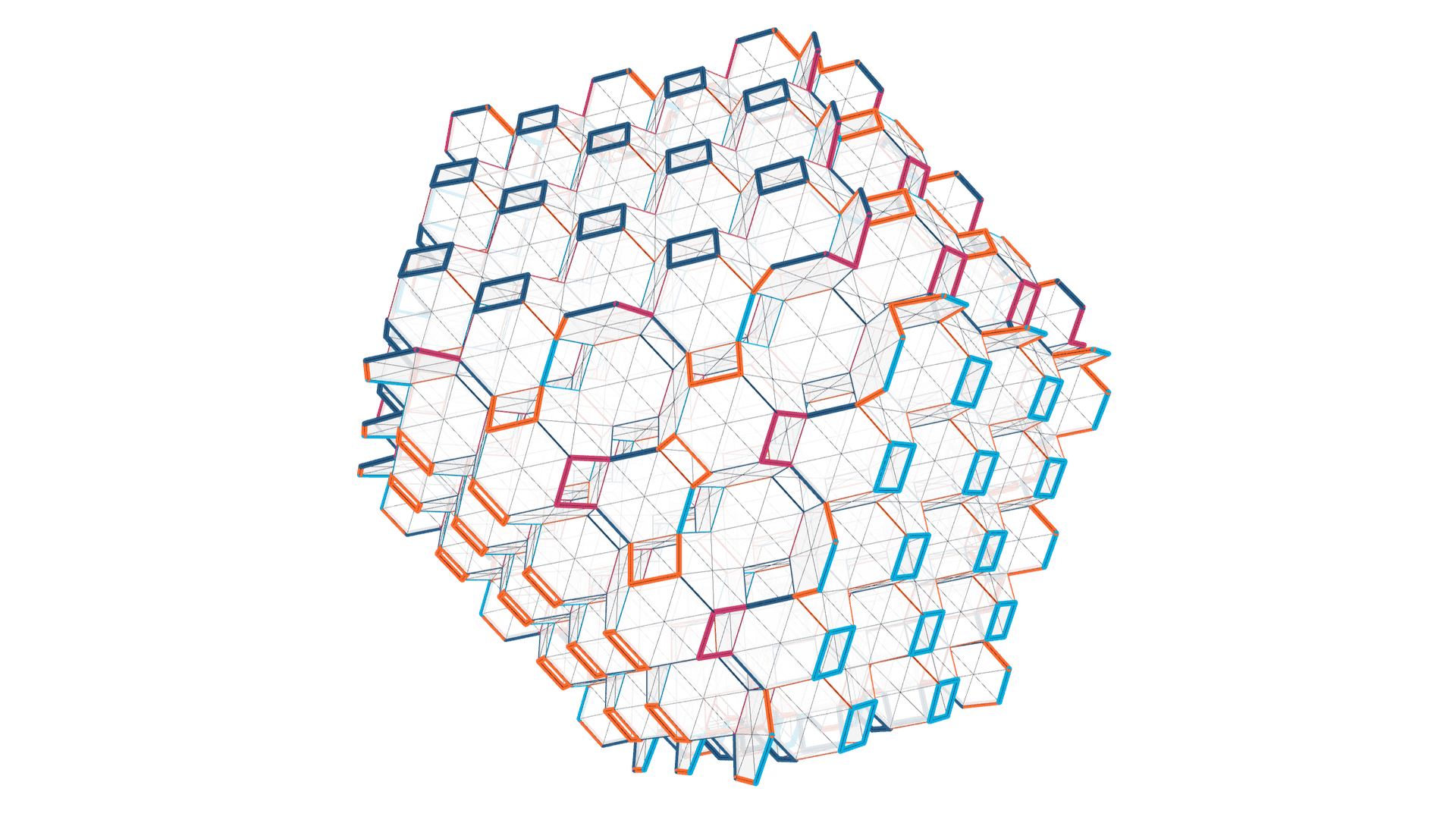
The mucube, somewhat astonishingly, turned out to be much more evasive.

Within a combinatorial framework of abstract polygons we are not necessarily bound to the classic way of thinking about polytopes, where these are constructed geometrically via planar polygons. Our structures are primarily combinatorial and graph like. Geometry enters the picture as an afterthought, if you like. Constructing a combinatorial cube therefore becomes a matter of finding a graph structure that can be embedded on the surface of the cube in such a way that faces are congruent and nodes map to vertices. Thus we can look for meta structures, further refineable using geometric infratilings (sub-tesselations of the combinatorial faces). The search for the mucube proved to be a perfect example of the use of such a procedure.

While representations of the mucube clearly suggest that its geometric structure is based upon squares, it was not until I started experimenting with transpositional tiles of more than four edges that a solution was found.

Several approaches were taken based on studies of the mucube geometry, like using units based on skew hexagonal tiles with edges incident to the diagonals of the squares or mapping edges of a dodecagonal tile to the regular edges of the mucube, while letting it cover six squares at a time. Both approaches lead to dead ends. The much more unlikely candidate, which finally lead to a solution for the mapping problem, was an octagonal tile.

Not only the fact that the transpositional tiling of the mucube should be based on an octagonal meta structure came as a surprise, also the way this tiling helps elucidate the tight geometric and combinatorial relationship between the mucube and the muoctahedron.

The geometry of the skew octagons one would need to be looking for in order to form the mucube is quite clear.

Take a regular unit square. On two opposing edges of the square add isosceles triangles pointing upwards, away from the square's plane in a 90 degree angle with equal leg lengths of $\sqrt 2 \over 2$. On the other two edges add the same size triangles pointing down. We thus get a skew octagon by adding four new vertices to the four given by the square.

Within the overall tiling four triangles can now be combined in a plane to create another square equal in size to our base square. Using this property, we can create a geometric tiling of the mucube, where half the vertices of the octagons would be incident to centres of the mucube squares, while the other half would come to lie on the corners of the squares.

Combinatorially, this means that half the vertices of this new tiling would be incident to four octagons, while three octagons would always come together at the other half of the vertices. As a consequence, the combinatorial requirements of the n-colouring needed are given and we can pick matching tiles from the list of 8-colorings.

The 8-colouring $4t^1$ for example matches the requirements. Additionally, one could argue that, with four consecutive edge pairs of same transpositional colour, this highly symmetric n-colouring already hints at a tetragonal structure.

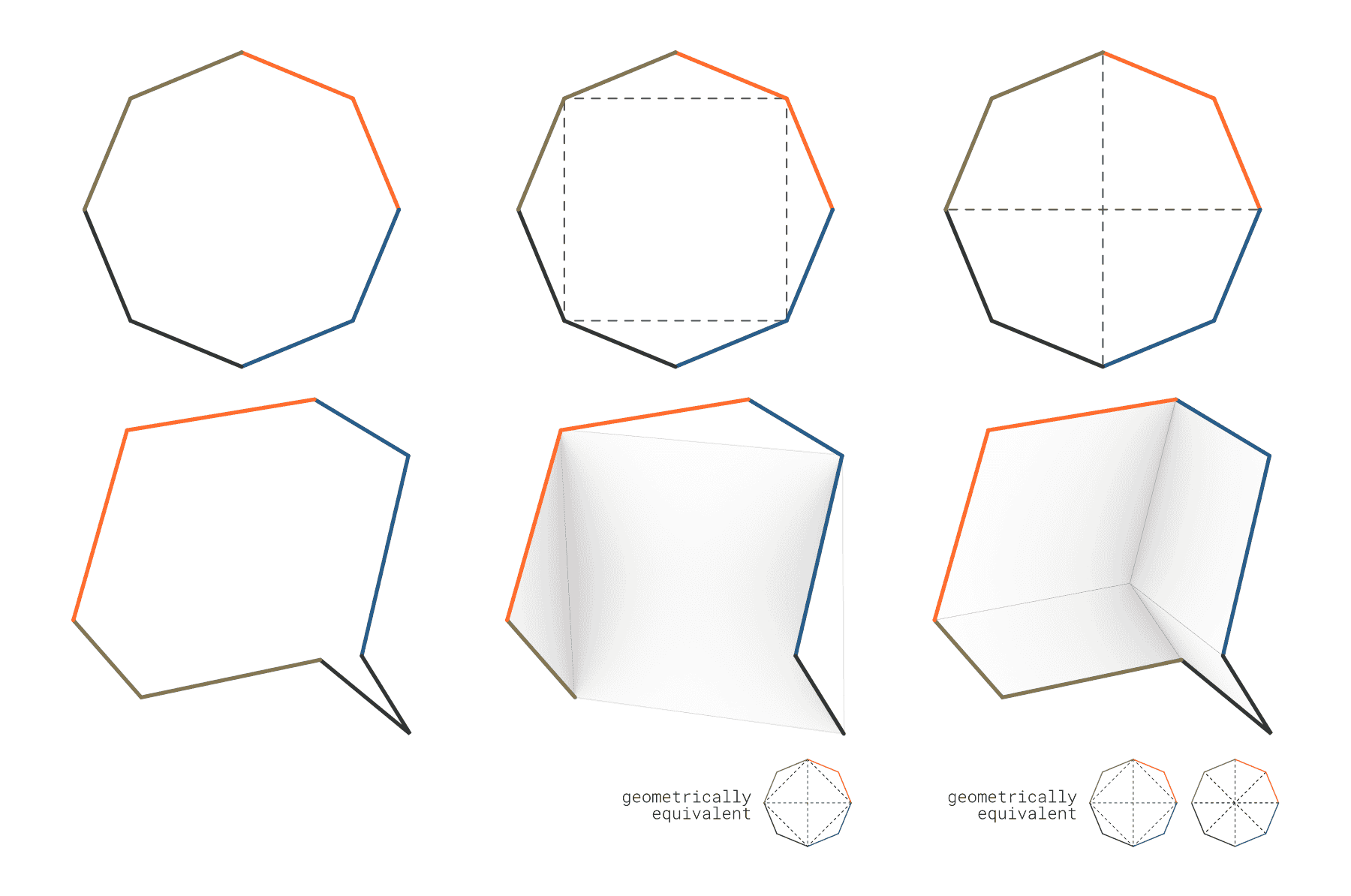
In the the left hand column of the figure above, the 8-coloring $4t^1$ can be found illustrated as a mapping onto the edges of the described skew geometry of the octagonal tile, while the center column shows the same geometry, with infratiling and thus faces in place. The right hand column showns another possible subdivision, we will come back to later. Important to note is, that the chosen mapping of the colors to the edges of the geometry is essential for the right geometrical properties to converge with the combinatorial effects given by the n-colouring and thereby make the covering of the mucube possible.

Armed with the basic geometric and combinatorial setup of our tile, we can now search for possible looping cycles and find that $2*(t_1-,t_4-)$,$2*(t_1+,t_2+)$,$2*(t_3-,t_2-)$ and $2*(t_3+,t_4+)$ will create the required tilegraph. Combined with the infratiling and geometry of the base tile described above, this tilegraph yields the mucube surface.

Thus the goal of creating the mucube using transpositional tiling has already been reached and we could stop there. Surprisingly though, not only the mucube is hiding in this octagonal structure.

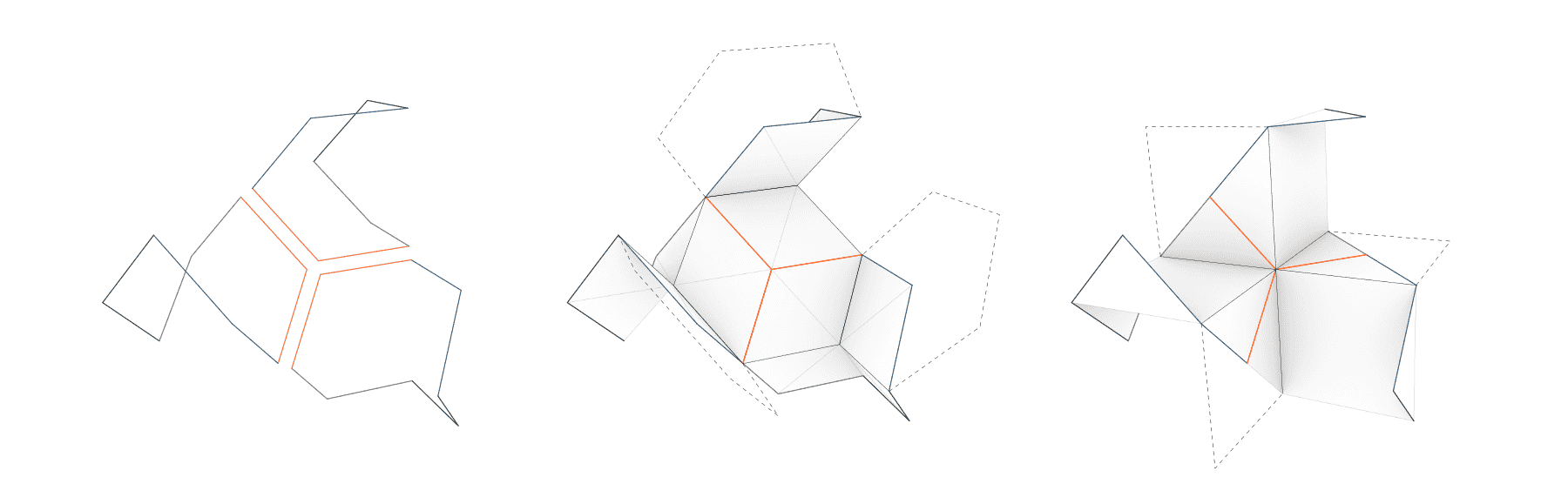
Look closely at the following illustration of the tilegraph and take the 3d model for a spin.

This does not look like the mucube at all. Rather than squares one finds hexagons to be the most easily identifiable face in the tilegraph. Which hints at the muoctahedron, rather than the mucube.

What is going on?

Instead of the chordal infratiling already described, we are using the alternative shown above to the right, in the example. The octagons have been split into 4 kites all connected at the center, which can in turn be split into two triangles.

Whether we will get a mucube or a mutetrahedron is a matter of tesselating the octagons in one way or the other. In terms of the combinatorics and how we put the overall meta-tilegraph together there is no difference. The tilegraph is the same. Thus by flip-flopping the four infratiling edges from a chordal to a centroidal orientation you can transform the mucube into a muoctahedron and vice versa. The geometry of the octagonal lattice remains the same, which implies that it must be possible to intersect the two infinite polyhedra to get the edge lattice of the octagonal tilegraph. The centers of the faces of one become the vertices of the other, as can be seen below. A notion of reciprocity that was already described by coxeter.

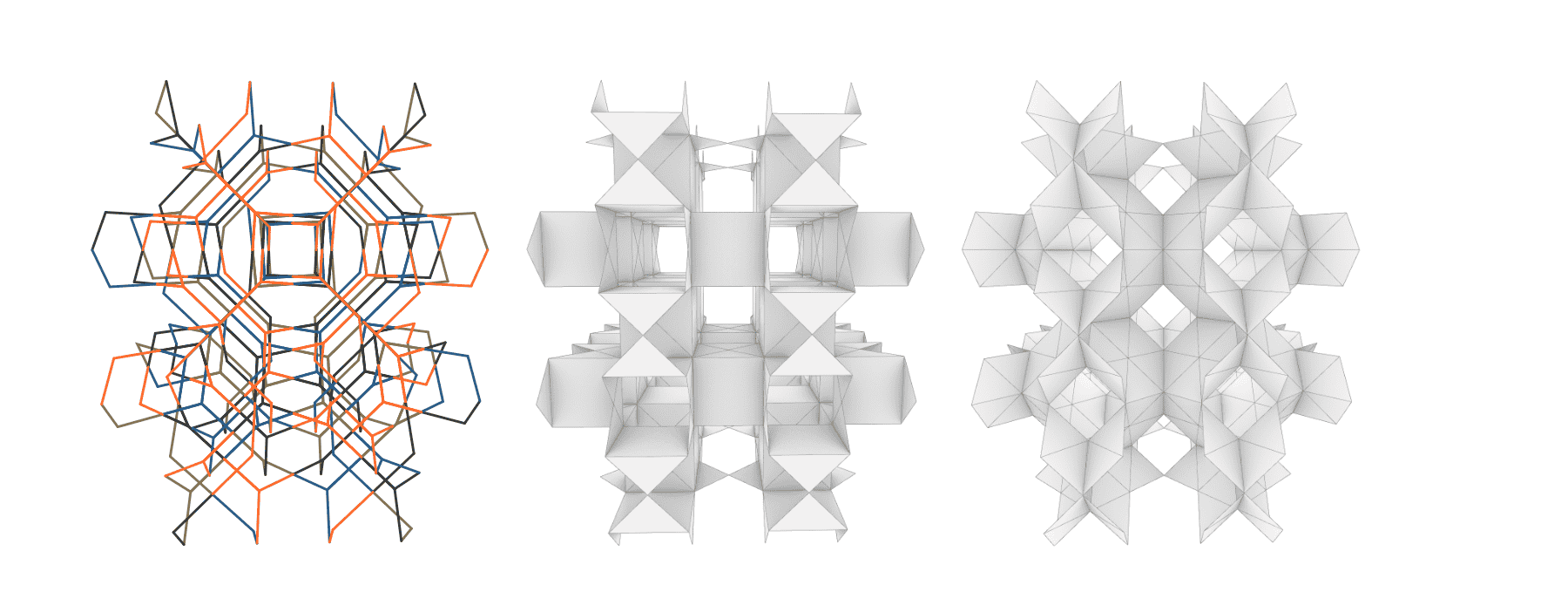
The ability to describe these two apeirohedra, which seem so intuitively related to squares and hexagons, using the same octagonal scaffolding, beautifully hints at the potential of using the transpositional topology framework to analyse deeper combinatorial relationships, even in already well known poly- and apeirotopes.

And even more surprises can be had.

Since we have a coloring of the edges, a natural question is, how the structure will change if single colors/edges are removed.

Take away two of the colors of the octagons, either $t_1$ and $t_3$ or $t_2$ and $t_4$ to produce the laves lattice with its characteristic spirals, which is the underlying skeleton of the gyroid minimal surface. The following illustration shows the regular octagonal lattice to the left and the two versions of the laves graph in the center and to the right.

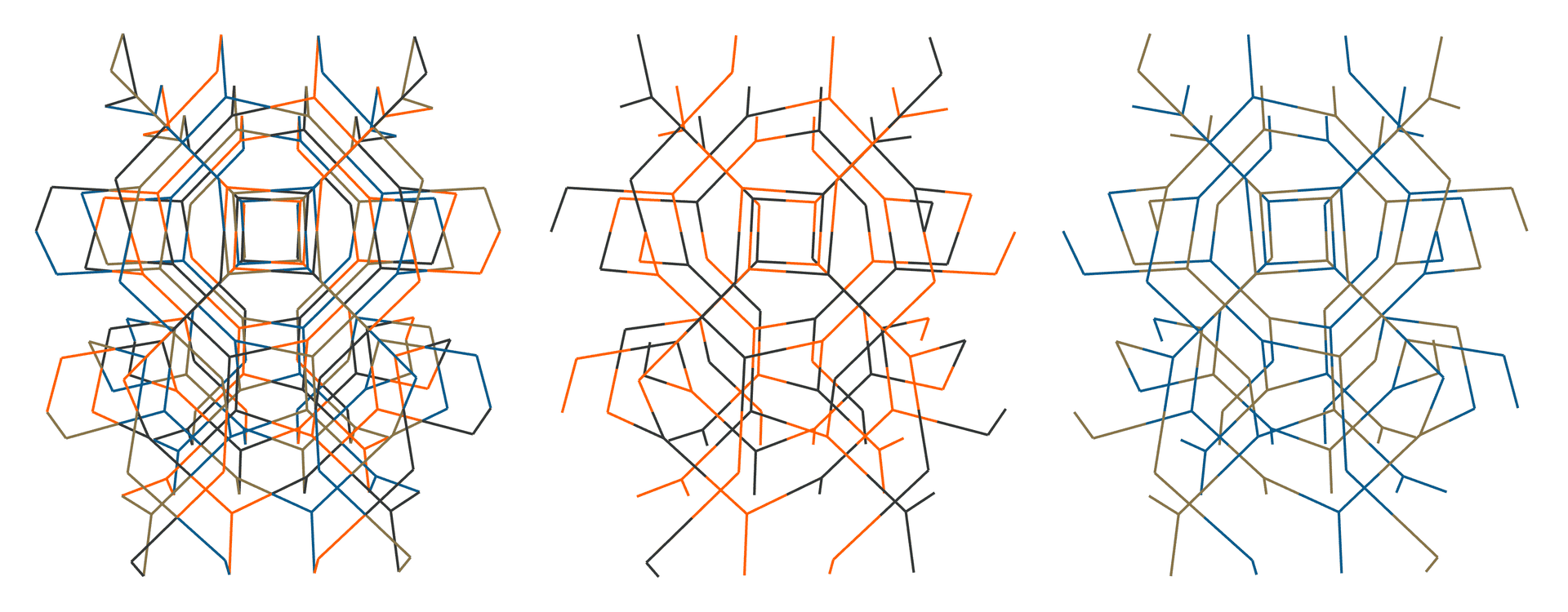
A beautiful fact and a stroke of luck to be able to finish with a trompe-l'œil.